The temperature at which the given reaction is at equilibrium Ag2Os→2Ag(s)+12O2(g)
ΔH=40.5kJmol−1 and ΔS=0.086kJmol−1K−1
470.93 K
362.12 K
262.12 K
562.12 K
The correct Answer is:A
To find the temperature at which the given reaction is at equilibrium, we can use the Gibbs free energy equation:
ΔG=ΔH−TΔS
At equilibrium, the change in Gibbs free energy (ΔG) is zero. Therefore, we can set up the equation as follows:
0=ΔH−TΔS
Rearranging this equation to solve for temperature T:
T=ΔHΔS
Step 1: Identify the values of ΔH and ΔS
From the question, we have:
- ΔH=40.5kJ/mol
- ΔS=0.086kJ/mol K
Step 2: Substitute the values into the equation
Now, we can substitute the values into the equation we derived for T:
T=40.5kJ/mol0.086kJ/mol K
Step 3: Perform the calculation
Calculating the temperature:
T=40.50.086≈470.93K
Conclusion
The temperature at which the reaction is at equilibrium is approximately 470.93K.
---
- ΔH=40.5kJ/mol
- ΔS=0.086kJ/mol K
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH INSTITUTECHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (Section - C) Previous Years Questions
60 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTECHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (Section -D) Assertion-Reason Type Questions
15 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTECHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (Section - A) Objective Type Questions
55 Videos
- THE SOLID STATE BOOK - AAKASH INSTITUTECHAPTER - THE SOLID STATE EXERCISE - Assignment (SECTION - D) (ASSERTION-REASON TYPE QUESTION)
20 Videos
Similar Questions
Knowledge Check
The temperature at which the reaction : Ag2O(s)→2Ag(s)+1/2O2(g) is at equilibrium is ……..,
Given ΔH=30.5KJmol−1
and ΔS=0.5KJmol−1 :A462.12KB362.12KC262.12KD562.12KThe temperature at which the reaction,
Ag2O(s)→2Ag(s)+1/2O2(g)
Is at equilibrium is ..., Given ΔH=30.5KJmol−1 and ΔS =0.066KJK−1A462.12KB362.12KC262.12KD562.12KCalculate the free energy change for the following reaction at 300 K.
2CuO(s)→Cu2O(s)+12O2(g) Given ΔH=145.6kJmol−1 and ΔS=116.JK−1mol−1A110.8kJmol−1B221.5kJmol−1C55.4kJmol−1D145.6kJmol−1
Calculate the temperature at which liquid water will be in equilibrium with water vapour.
ΔvapH=40.00kJmol−1 and ΔvapS=0.100kJmol−1K−1
View SolutionCalculated the equilibrium constant for the following reaction at 298K:
2H2O(l)→2H2(g)+O2(g)
ΔfGΘ(H2O)=−237.2kJmol−1,R=8.314Jmol−1K−1
View SolutionCalculate the equilibrium constant, K for the following reaction at 400K?
2NOCl(g)⇔2NO(g)+Cl2(g)
Given that ΔrH0=80.0KJmol−1 and ΔrS0=120JK−1mol−1 at 400 K.
View SolutionΔH and ΔS for the reaction:
Ag2O(s)→2Ag(s)+(1/2)O2(g)
are 30.56kJmol−1 and 66.0JJK−1mol−1 respectively. Calculate the temperature at which free energy change for the reaction will be zero. Predict whether the forward reaction will be favoured above or below this temperature.
View SolutionFor a reversible reaction at constant temperature and at constant pressure the equilibrium composition of reaction mixture corresponds to the lowest point on Gibbls energy Vs progress of reaction diagrams as shown. At equilibrium Gibbs energy of reaction is equal to zero.
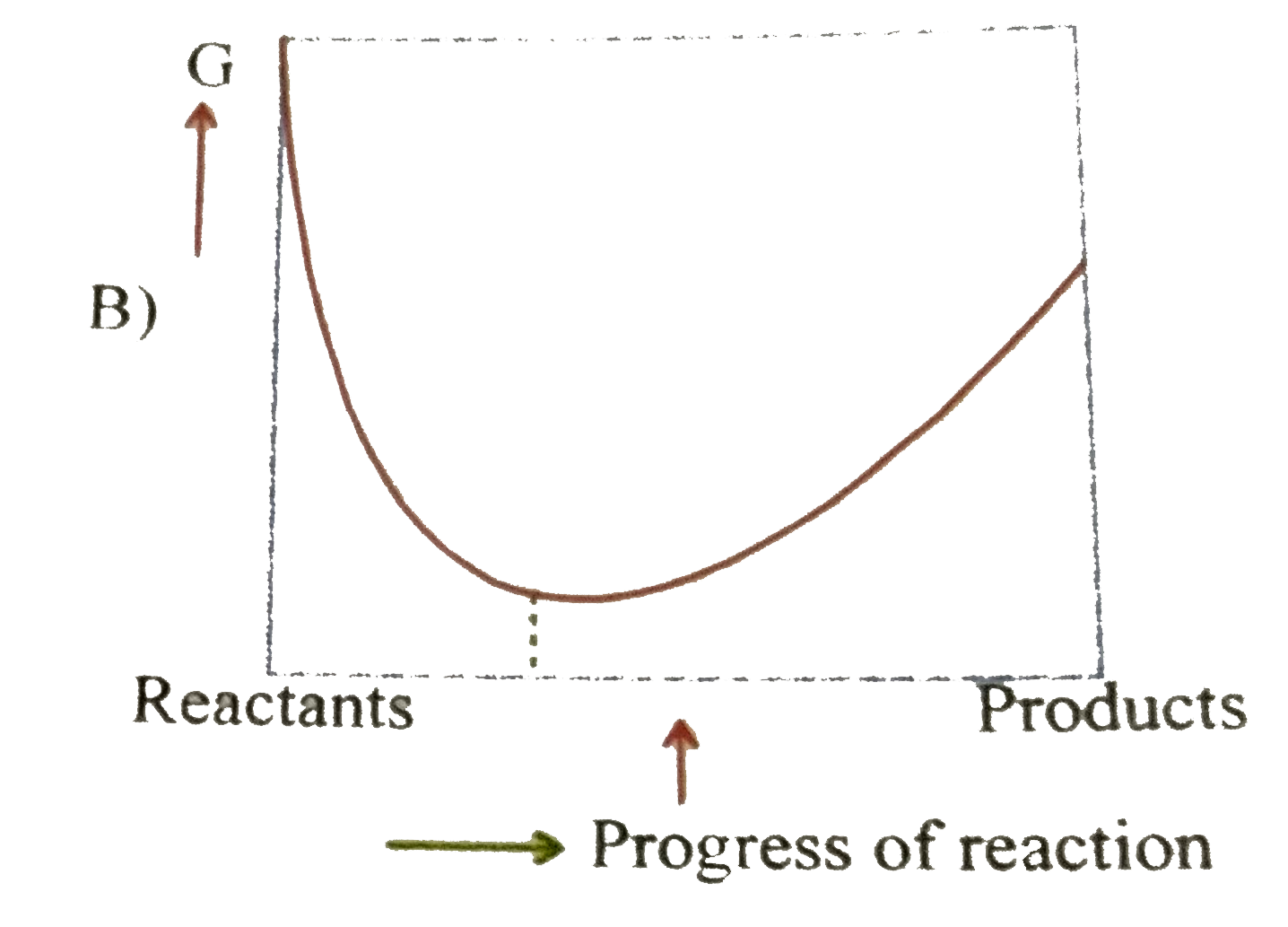
For a reaction
M2O3/4(s)→2M(S)+12O2(g)ΔH=30KJ/mol and ΔS=0.07KJ/mol/K at 1 atm. The reaction would not be spontaneous at temperature
View Solution
