Three metals A, B and C are arranged in increasing order of standard reduction electrode potential, hence their chemical reactivity order will be
A<B<C
A>B>C
B>C>A
A=B=C
The correct Answer is:B
To determine the chemical reactivity order of metals A, B, and C based on their standard reduction potentials (SRP), we can follow these steps:
Step 1: Understand Standard Reduction Potential
Standard reduction potential (SRP) is a measure of the tendency of a chemical species to gain electrons and be reduced. Metals with lower SRP values are more likely to lose electrons and act as reducing agents, while those with higher SRP values are more likely to gain electrons and act as oxidizing agents.
Step 2: Arrange Metals by SRP
According to the problem, the metals are arranged in increasing order of their standard reduction potentials:
- A < B < C
This means:
- Metal A has the lowest SRP (most reactive)
- Metal B has a medium SRP
- Metal C has the highest SRP (least reactive)
Step 3: Determine Reactivity Order
Since metals with lower SRP are more reactive (they can easily lose electrons), we can conclude that:
- Metal A is the most reactive.
- Metal B is less reactive than A but more reactive than C.
- Metal C is the least reactive.
Step 4: Write the Reactivity Order
From the above analysis, the order of reactivity from most reactive to least reactive is:
- A > B > C
Final Answer
The chemical reactivity order of metals A, B, and C is:
A > B > C
---
Standard reduction potential (SRP) is a measure of the tendency of a chemical species to gain electrons and be reduced. Metals with lower SRP values are more likely to lose electrons and act as reducing agents, while those with higher SRP values are more likely to gain electrons and act as oxidizing agents.
According to the problem, the metals are arranged in increasing order of their standard reduction potentials:
- A < B < C
This means:
- Metal A has the lowest SRP (most reactive)
- Metal B has a medium SRP
- Metal C has the highest SRP (least reactive)
Since metals with lower SRP are more reactive (they can easily lose electrons), we can conclude that:
- Metal A is the most reactive.
- Metal B is less reactive than A but more reactive than C.
- Metal C is the least reactive.
From the above analysis, the order of reactivity from most reactive to least reactive is:
- A > B > C
The chemical reactivity order of metals A, B, and C is:
A > B > C
Topper's Solved these Questions
- REDOX REACTIONSBOOK - AAKASH INSTITUTECHAPTER - REDOX REACTIONSEXERCISE - ASSIGNMENT SECTION - C
23 Videos
- REDOX REACTIONSBOOK - AAKASH INSTITUTECHAPTER - REDOX REACTIONSEXERCISE - ASSIGNMENT SECTION - D
10 Videos
- REDOX REACTIONSBOOK - AAKASH INSTITUTECHAPTER - REDOX REACTIONSEXERCISE - ASSIGNMENT SECTION - A
35 Videos
- PRINCIPLES OF QUALITATIVE ANALYSISBOOK - AAKASH INSTITUTECHAPTER - PRINCIPLES OF QUALITATIVE ANALYSISEXERCISE - Assignment (SECTION H)
9 Videos
- SOLUTIONSBOOK - AAKASH INSTITUTECHAPTER - SOLUTIONSEXERCISE - ASSIGMENT (SECTION-J) AAKASH CHALLENGERS QUESTIONS
10 Videos
Similar Questions
Knowledge Check
K,Ca and Li metals may be arranged in the decreasing order of their standard electrode potentials as
AK,Ca,LiBLi,K,CaCLi,Ca,KDCa,Li,KK,Ca and Li metals may be arranged in the decreasing order of their standard electrode potentials as
AK, Ca, LiBCa, K, LiCLi, Ca, KDCa, Li, KWhich defines the standard reduction electrode potential of Zn2+ ions
AZn2+(aq)+2e−→Zn(s),[Zn2+]=1MBZn(g)→Zn2++2e−,[Zn2+]=1MCZn2+(aq)→Zn(s)+2e−,[Zn2+]=1MDZn2+(g)+2e−→Zn(s)−2e−,[Zn2+]=1M
Arrange in decreasing order of reactivity with HCl :
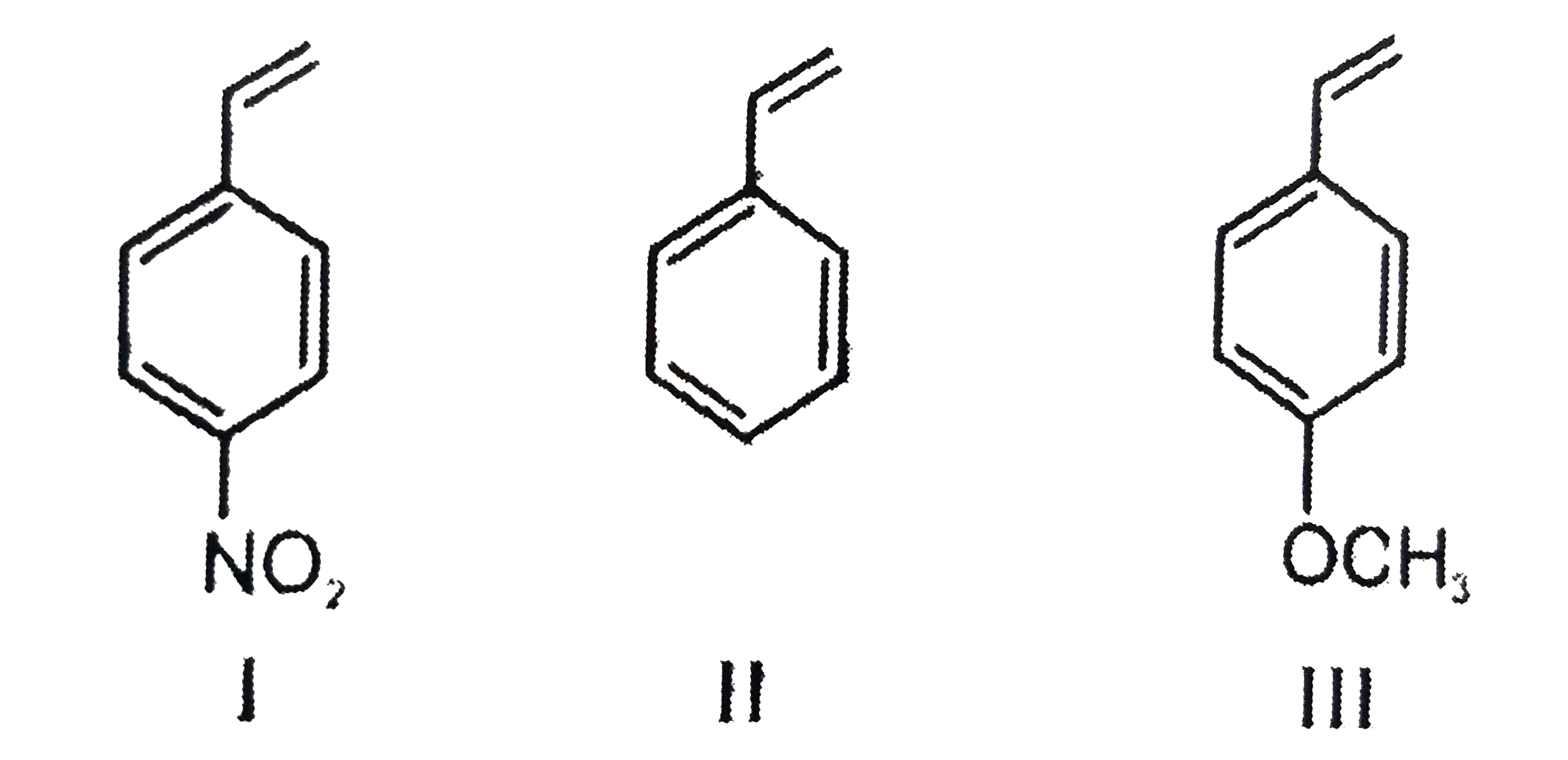
View SolutionLi, Ca and K metals can be arranged in the decreasing order of their standard reduction potentials as __________.
View SolutionArrange the metals Ca, Al, Mg and Zn in decreasing order of their reactivities :
View SolutionThe correct order of increasing chemical reactivity is
View SolutionMost of the metals react chemically with other substances in one form or another. Few metals which do not react with common chemicals are called noble metals e.g., silver, gold, platinum. The rate of reaction with which metals react is not same for all the metals. The rate of reaction depends on the reactivity of metals. On the basis of their reactive nature, a series known as reactivity series has been drawn in which metals are arranged in decreasing order of their reactivity.

Which of the following represents the correct reactivity order of metals with water?
View Solution
