Question

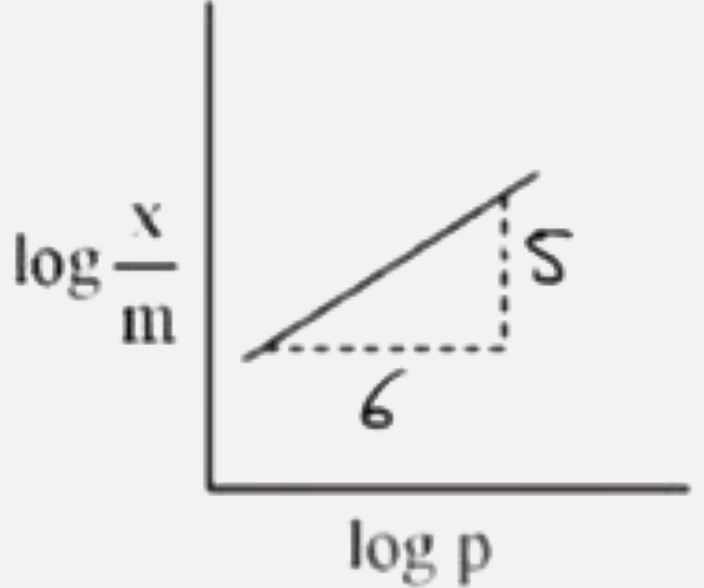
The intercept on Y - axis in the graph of log ${\displaystyle \frac{x}{m}}$ versus log P gives

Options

A. `(1)/(n) (n gt 1)`
B. k
C. log k
D. Temperature

Answer

C

Explanation

To solve the question regarding the intercept on the Y-axis in the graph of log $$\left(x/m\right)$$ versus log $$P$$, we can follow these steps:

1. Understanding the Variables:
- Let \(x\) be the mass of the adsorbate.
- Let \(m\) be the mass of the adsorbent.
- The term \(\frac{x}{m}\) represents the degree of adsorption.

2. Establishing the Relationship:
- The degree of adsorption \(\frac{x}{m}\) is proportional to the pressure \(P\) raised to the power of \(\frac{1}{n}\), where \(n\) is a constant. This can be expressed as:
\( \frac{x}{m} \propto P^{\frac{1}{n}} \)

3. Converting to Logarithmic Form:
- To express this relationship in logarithmic form, we can write:
\( \frac{x}{m} = k \cdot P^{\frac{1}{n}} \)
- Taking the logarithm of both sides gives:
\( \log\left(\frac{x}{m}\right) = \log(k) + \frac{1}{n} \log(P) \)

4. Identifying the Linear Form:
- This equation resembles the linear equation \(y = mx + c\), where:
- \(y = \log\left(\frac{x}{m}\right)\)
- \(m = \frac{1}{n}\) (the slope)
- \(c = \log(k)\) (the y-intercept)

5. Conclusion:
- From the above expression, we can conclude that the intercept on the Y-axis (when plotting \(\log\left(\frac{x}{m}\right)\) versus \(\log(P)\)) is:
\( \text{Intercept} = \log(k) \)

Final Answer:
The intercept on the Y-axis in the graph of \(\log\left(\frac{x}{m}\right)\) versus \(\log(P)\) gives \(\log(k)\).