Prove that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
Step by step video & image solution for Prove that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The sum of the three vectors determined by the medians of triangle directed from the vertices is
A0B1C−1D13The point where the all three medians of a triangle meet is called
ACentroidBIncentreCCircumcentreDOrthocentre
The sum of these three vectors is :
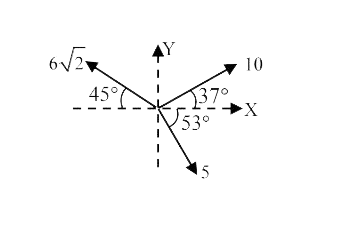
View SolutionThree coinitial vectors of magnitudes a, 2a and 3a meet at a point and their directions are along the diagonals if three adjacent faces if a cube. Determined their resultant R. Also prove that the sum of the three vectors determinate by the diagonals of three adjacent faces of a cube passing through the same corner, the vectors being directed from the corner, is twice the vector determined by the diagonal of the cube.
View SolutionProve that the sum of the vectors directed from the vertices to the mid-points of opposite sides of a triangle is zero.
View SolutionProve that the sum of the three exterior angles of a triangle, formed by producing the sides in order, is 4 right angles.
View SolutionProve that the sum of three altitudes drawn from the vertices to opposite sides of a triangle is less than the sum of three sides.
or
Prove that the perimeter of a triangle is greater than the sum of three altitudes drawn from the vertices to opposite of a triangle.
View SolutionProve that the sum of the three angles of a triangle is 1800.
View Solution
