Column I, Column II Collinear vectors, p. $\to a$ Coinitial vectors, q. $\to b$ Equal vectors, r. $\to c$ Unlike vectors (same intitial point), s. $\to d$

Video Solution

Answer

Step by step video & image solution for Column I, Column II Collinear vectors, p. vec a Coinitial vectors, q. vec b Equal vectors, r. vec c Unlike vectors (same intitial point), s. vec d by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Knowledge Check

If $\to P and \to Q$ are two vectors, then the value of $(\to P + \to Q) \times (\to P - \to Q)$ is
A $\to P \times \to Q$
B $- (\to P \times \to Q)$
C $2 (\to Q \times \to P)$
D $+ 2 (\to P \times \to Q)$

If $\to a$ is a unit vector, $\to a \times \to r = \to b, \to a \cdot \to r = c, \to a \cdot \to b = 0$ then $\to r$ is equal to
View Solution
If $\to a$ is a unit vector, $\to a \times \to r = \to b, \to a \cdot \to r = c, \to a \cdot \to b = 0$ , then $\to r$ is equal to
View Solution
Find the angle between the vectors $\to a = 2 \to p + 4 \to q$ and $\to b = \to p - \to q$ where $\to p$ and $\to q$ are unit vectors forming an angle of $120^{\circ}$ .
View Solution
If $\to a$ and $\to b$ are orthogonal unit vectors, then for a vector $\to r$ noncoplanar with $\to a$ and $\to b$ , vector $r \times a$ is equal to a. $[\to r \to a \to b] \to b - (\to r . \to b) (\to b \times \to a)$ b. $[\to r \to a \to b] (\to a + \to b)$ c. $[\to r \to a \to b] \to a - (\to r . \to a) \to a \times \to b$ d. none of these
View Solution
What is the unit vector $ˆ a$ parallel to the vector $\to a = 3 \to I + 4 \to j - 2 \to k$ ? Find the vector $\to b$ such that $ˆ a + \to b$ becomes the unit vector $\to i$ ?
View Solution
Given below in Column I are the relations between vectors a,b and c and in Column II are the orientations of a, b and c in the XY - plane . Match the relation in Column I to correct orientations in Column II.

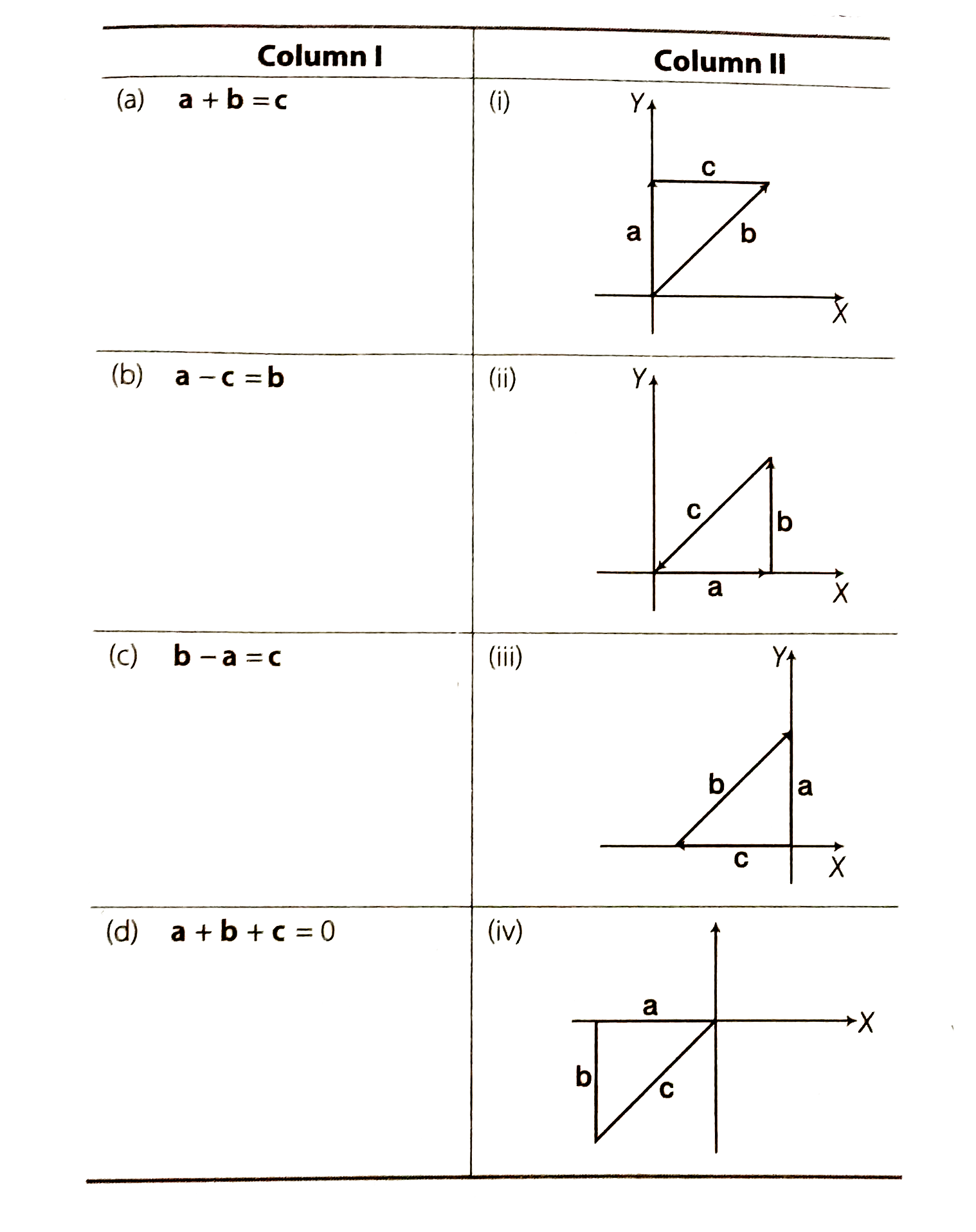
View Solution
Suppose that $\to p, \to q and \to r$ are three non-coplanar vectors in $R^{3}$ . Let the components of a vector $\to s$ along $\to p, \to q and \to r$ be 4, 3 and 5, respectively. If the components of this vector $\to s$ along $(- \to p + \to q + \to r), (\to p - \to q + \to r) and (- \to p - \to q + \to r)$ are x, y and z, respectively, then the value of $2 \to x + \to y + \to z$ is
View Solution

Column I, Column II Collinear vectors, p. $\to a$ Coinitial vectors, q. $\to b$ Equal vectors, r. $\to c$ Unlike vectors (same intitial point), s. $\to d$

Similar Questions

Knowledge Check

If $\to P and \to Q$ are two vectors, then the value of $(\to P + \to Q) \times (\to P - \to Q)$ is

Recommended Questions

Column I, Column II Collinear vectors, p.→a Coinitial vectors, q. →b Equal vectors, r. →c Unlike vectors (same intitial point), s. →d

Similar Questions

Knowledge Check

If →Pand→Q are two vectors, then the value of (→P+→Q)×(→P−→Q) is

Recommended Questions

Column I, Column II Collinear vectors, p. $\to a$ Coinitial vectors, q. $\to b$ Equal vectors, r. $\to c$ Unlike vectors (same intitial point), s. $\to d$

If $\to P and \to Q$ are two vectors, then the value of $(\to P + \to Q) \times (\to P - \to Q)$ is