The midpoint of two opposite sides of a quadrilateral and the midpoint of the diagonals are the vertices of a parallelogram. Prove that using vectors.
Step by step video & image solution for The midpoint of two opposite sides of a quadrilateral and the midpoint of the diagonals are the vertices of a parallelogram. Prove that using vectors. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
View SolutionIf the opposite sides of a quadrilateral are equal, prove that the quadrilateral is a parallelogram.
View Solution
Knowledge Check
If the opposite sides of a quadrilateral and also its diagonals are equal, then each of the angles of the quadrilateral is
A90∘B120∘C100∘D60∘If the opposite sides of a quadrilateral and also its diagonals are equal, then each of the angles of the quadrilateral is
A90∘B120∘C100∘D60∘The midpoints of the sides of a triangle along with any of the vertices as the fourth point makes a parallelogram of area equal to
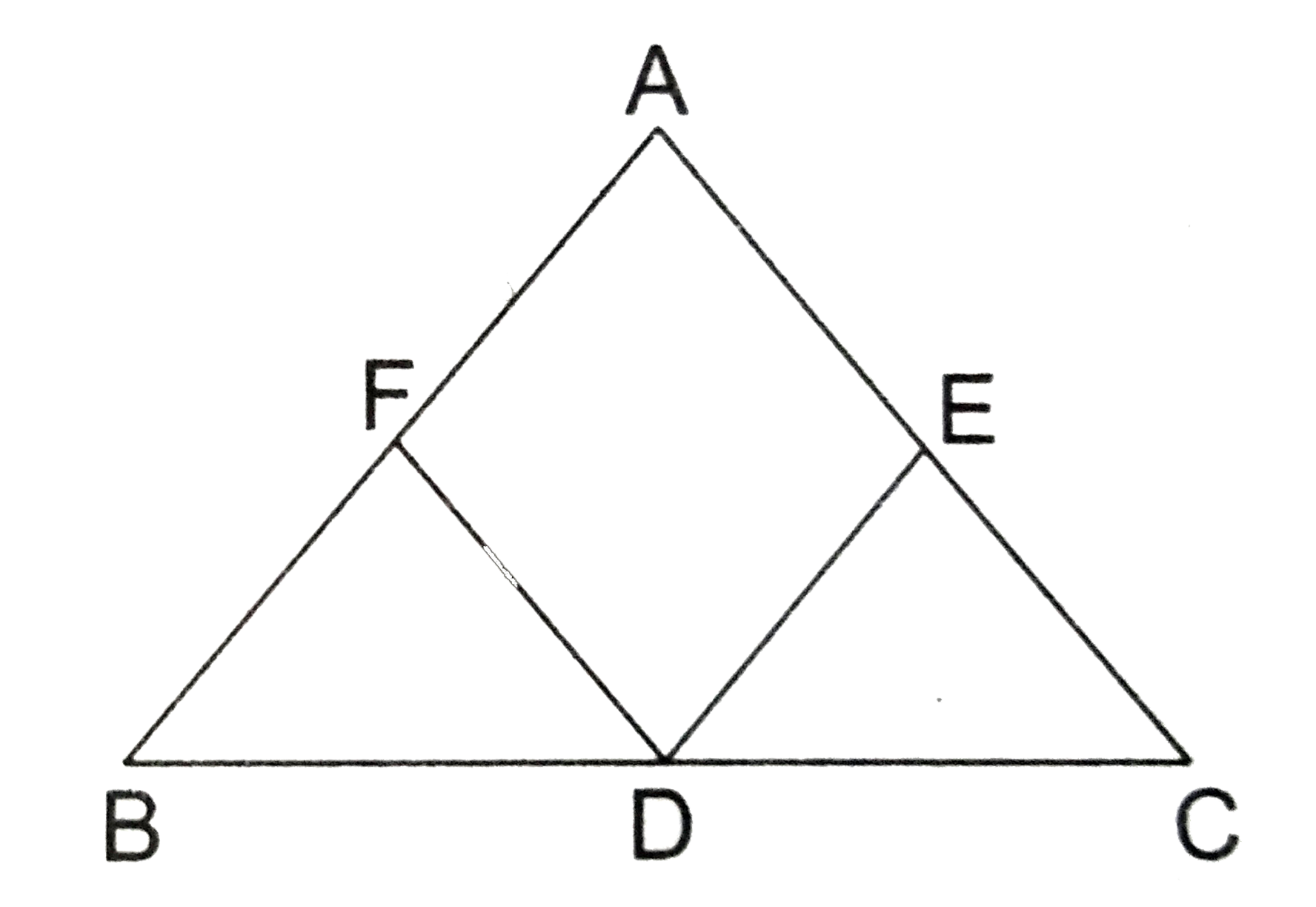 A2(ar△ABC)B13(ar△ABC)C14(ar△ABC)Dar(△ABC)
A2(ar△ABC)B13(ar△ABC)C14(ar△ABC)Dar(△ABC)
If two opposite sides of a cyclic quadrilateral are equal, then the other two sides are parallel.
View SolutionProve that the lines joining the middle points of opposite sides of a quadrilateral and the line joining the middle points of its diagonals meet in a point and bisect one another.
View SolutionIf two opposite sides of a cyclic quadrilateral are equal; then the other two sides are parallel.
View SolutionIf the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
View SolutionIf the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
View Solution
