The number of points, having both co-ordinates as integers, that lie in the interior of the triangle with vertices (0,0), (0,41) and (41,0) is
A
901
B
861
C
820
D
780
Video Solution
Text Solution
The correct Answer is:D
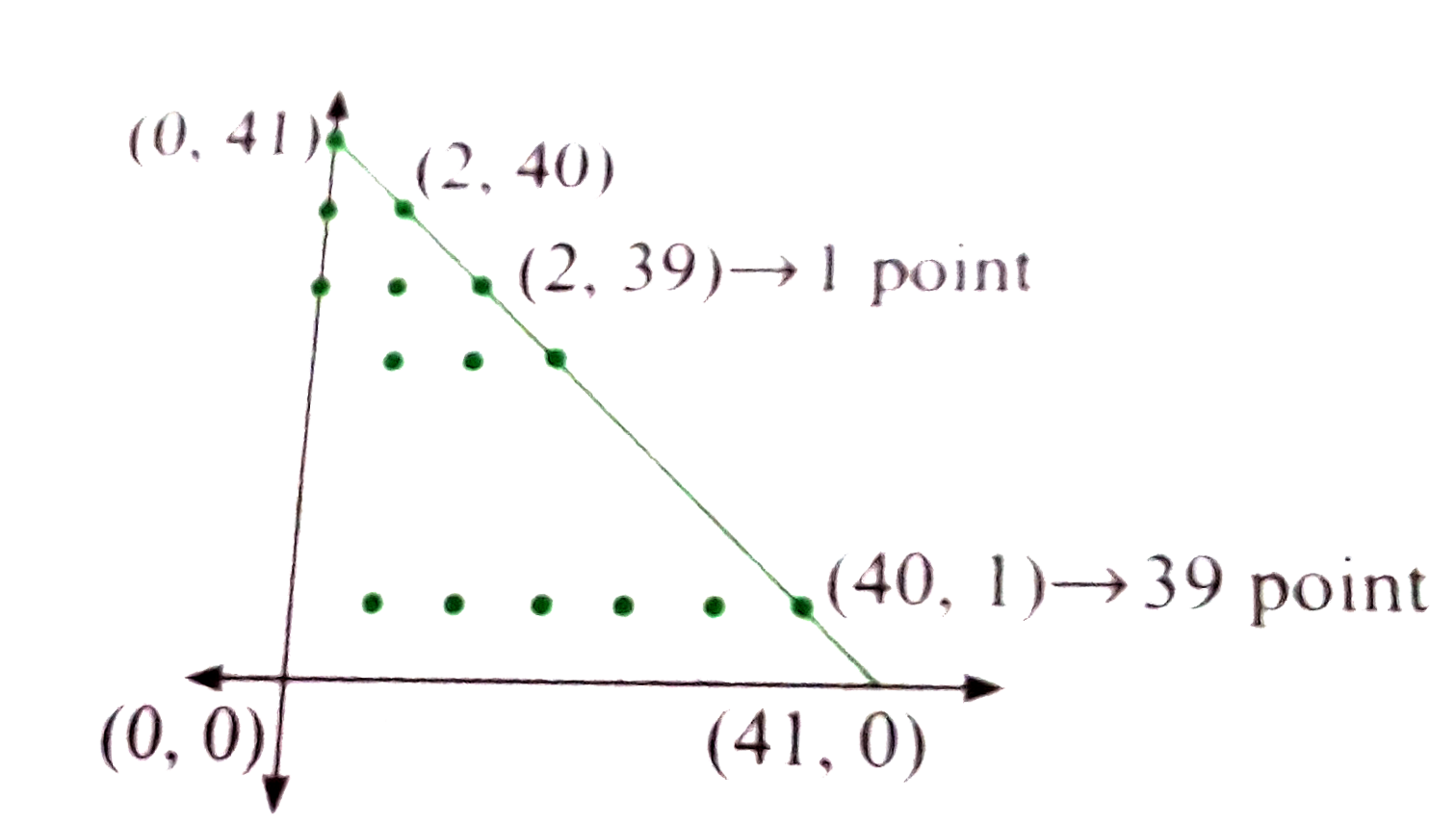
So number of points =1+2+3+..+39
39×402
=780
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The number of points, having both co-ordinates as integers, that line in the interior of the triangle with vertices (0, 0), (0, 41) and (41,0), is :
A901B861C820D780 - Question 2 - Select One
The number of points, having both coordinates are integers, that lie in the interior of the triangle with vertices (0,0), (0,41) and (41, 0) is
A901B861C820D780 - Question 3 - Select One
The perimeter of the triangle with vertices (0, 4), (0, 0) and (3, 0) is
A(7+√5)B5C10D12
The in-centre of the triangle with vertices (0,0),(1,0),(0,1) is
View SolutionThe triangle with vertices (0,0), (2,0) and (0,3) is
View SolutionThe circumcentre of the triangle with vertices (0, 0), (3, 0) and (0, 4) is
View SolutionThe number of integral points (integral point means both the coordinates should be integer) exactly in the interior of the triangle with vertices (0,0), (0,21) and (21,0) is
View SolutionThe nine point centre of the triangle with vertices (1,√3),(0,0) and (2, 0) is
View Solution

