Question

Solve the inequalities graphically in two-dimensional plane: $2x-3y>6$

Explanation

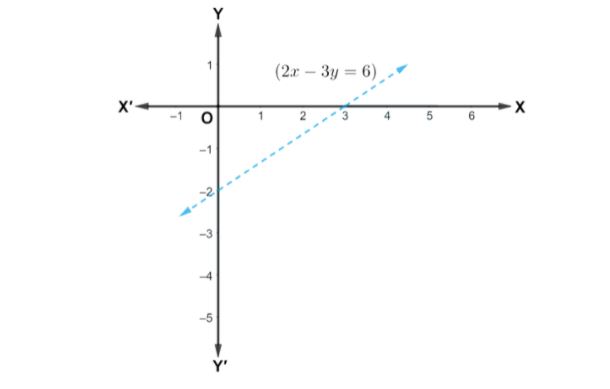
The graphical representation of `2x - 3y = 6` is given as a dotted line in the figure below.


This line divides the XY-plane into two half-planes.


Select a point (not on the line), which lies in one of the half-planes, to determine whether the point satisfies the given inequality or not.


We select the point as `(0, 0) `. It is observed that,


`2 (0) - 3(0) > 6` or `0 > 6` , which is false.


Therefore, the upper half-plane is not the solution region of the given inequality.


Also, any point on the line does not satisfy the given inequality


Thus, the solution region of the given inequality is the lower half-plane that does not contain the points including the line.



The solution region is represented by the shaded region as follows: