बिन्दु आवेश 30C,−20C तथा 10C, बिन्दुओं (−1,0,2),(0,0,0) तथा (1,5,−1) पर क्रमशः स्थित हैं। एक घन जिसकी भुजा 6m है तथा जिसका केन्द्र मूल बिन्दु पर केन्द्रित है, उस घन से पारित विद्युत फ्लक्स होगा।
−20ε0
10ε0
20ε0
30ε0
The correct Answer is:B
दिया है, बिन्दु आवेश 30C,−20C तथा 10c बिन्दु (−1,0,2),(0,0,0) तथा (1,5,−1) पर स्थित है। घन की भुजा =6m
गॉस प्रमेय से बन्द पृष्ठ से निर्गत् कुल विद्युत फ्लक्स qकुलε0
यहाँ पर 10C आवेश के निर्देशांक (1,5−1) है, जो कि घन के बाहर है।
अतः qकुल=30−20=10C
∴ कुल विद्युत फ्लक्स =qε0=10ε0
Topper's Solved these Questions
Similar Questions
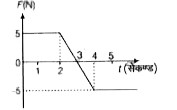
किग्रा द्रव्यमान का एक ब्लॉक x- अक्ष पर गतिमान है इस पर कार्यरत बल F चित्रनुसार है। समय t = 2 सेकण्ड पर ब्लॉक का वेग -3मी /से है , तो समय t = 4 सेकण्ड पर ब्लॉक की चाल क्या होगी ?
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionयदि एक समान्तरचतुर्भुज की आसन्न भुजाएँ ¯a तथा ¯b से निरूपित हैं जिसका क्षेत्रफल 15 वर्ग इकाई है, तो उस समान्तरचतुर्भुज का क्षेत्रफल जिसकी आसन्न भुजाएँ 3¯a+2¯b तथा ¯a+3¯b से निरूपित हैं, होगा :
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि बिन्दु (2,α,β) उस समतल पर स्थित है, जो बिन्दुओ (3,4,2) तथा (7,0,6) से होकर जाता है तथा समतल 2x−5y=15 के लंबवत है, तो 2α−3β बराबर है
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionउस सरल रेखा का समीकरण जो रेखाओं 3x-y+ 2 = 0 तथा 5x-2y+ 7 = 0 के प्रतिच्छेद बिन्दु से गुजरती है तथा जिसकी प्रवणता अनन्त है, होगा
View Solutionउस दीर्घवृत्त का समीकरण जिसका केंद्र मूलबिन्दु है तथा जो बिन्दुओं (-3, 1) तथा (2, -2) से गुजरता है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionउस गोले का समीकरण ज्ञात करो जो बिन्दुओं (1,0,0), (0, 1,0) तथा (0, 0, 1) से होकर गुजरता है तथा जिसका केन्द्र समतल 3x-y+z=2 पर स्थित हो।
View Solution
