Let A={u,v,w,x}. A bijective function f:A→A is chosen at random, then the probability that f(u)≠u,f(v)≠v,f(w)≠w and f(x)≠x is
Step by step video & image solution for Let A={u,v,w,x}. A bijective function f:A rarr A is chosen at random, then the probability that f(u)!=u,f(v)!=v,f(w)!=w and f(x)!=x is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
Let A={x,y,z}=B={u,v,w)andf:A→B be defined by f (x)=u,f(y)=v,f(z)=w. Then, f is
Asurjective but not injectiveBinjective but not surjectiveCbijectiveDnone of these - Question 2 - Select One
Let A = {x, y, z), B = {u, v, w} and f : A → B be defined by f(x) = u,
f(y) = v, f(z) = w. Then, f isAsurjective but not injectiveBinjective but not surjectiveCbijectiveDNone of the above - Question 3 - Select One
If u : v : w = 3 : 6 : 8, then what will be the ratio of (u/v) : (v/w) : (w/u)?
A8 : 6 : 3B8:4:3C5:9:12D6:9:32
Prove that ddx∣∣ ∣∣u1v1w1u2v2w2u3v3w3∣∣ ∣∣=∣∣ ∣∣u1v1w1u2v2w2u4v4w4∣∣ ∣∣ where u,v,w are functions of xanddudx=u1,d2udx2=u2, etc.
View SolutionLet W=N∪{0}. Suppose f:W→W is a function such that f(0)=0,f(1)=1,f(2)=2 and f(x)=f(x−2)+f(x−3) for x=3,4,……….. Then f(9) =……………..
View SolutionIf fandg are the function whose graphs are as shown, let u(x)=f(g(x)),w(x)=g(g(x))
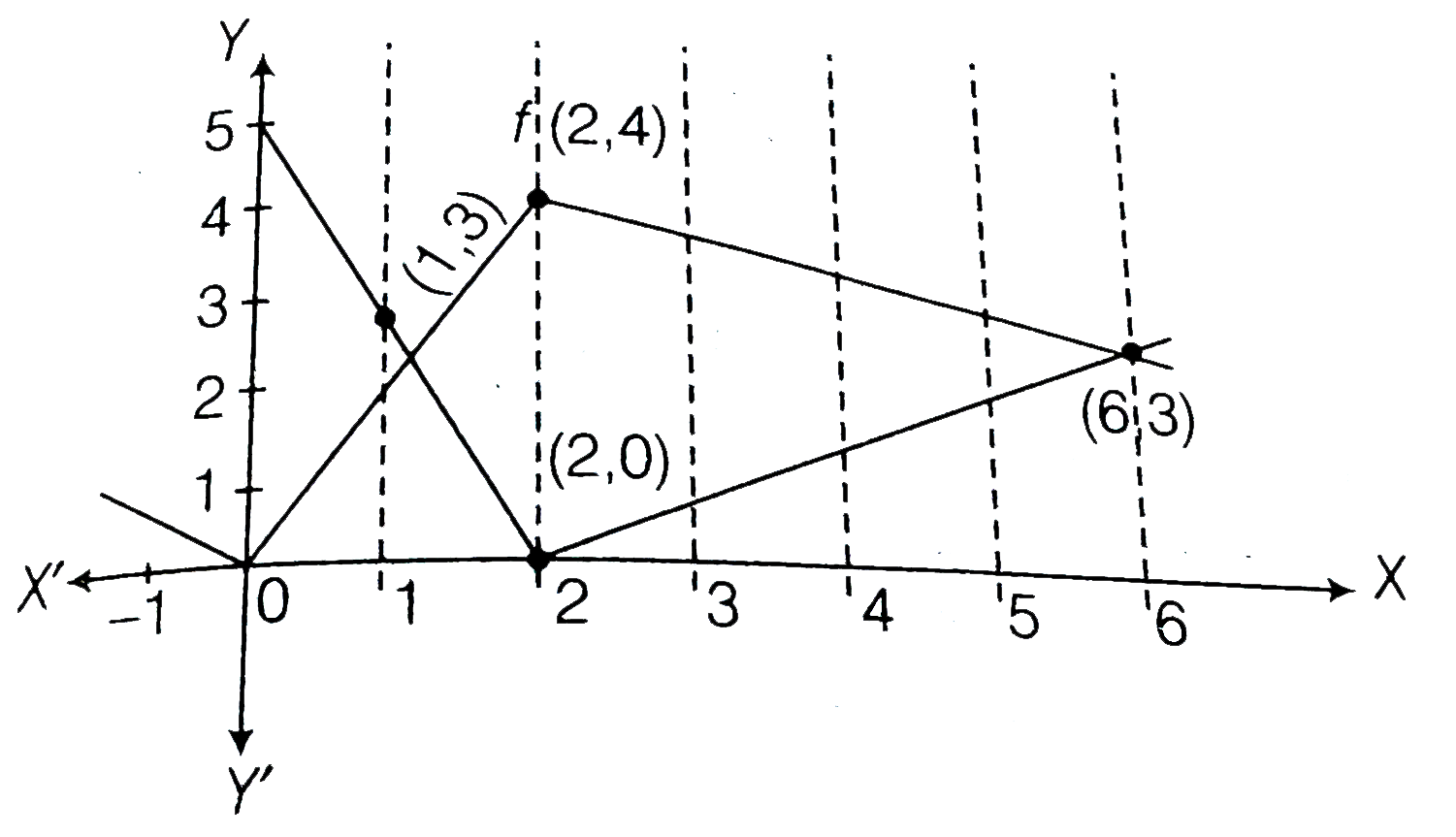 Then the value of u'(1)+w'(1) isView Solution
Then the value of u'(1)+w'(1) isView SolutionLet f:W→W be a given function satisfying f(x)=f(x−1)+f(x−2) for x≤2.If f(0)=0andf(1)=1 , ther find the value of f(2)+f(3)+f(4)+f(5)+f(6).
View SolutionX is the son of W and W is the brother of V. V is the sister of U. How is U related to X?
View Solution
