जैसा चित्र में दिखया गया है, एक खड़ी होने वाली सीढ़ी की दो पक्षों BA और CA की लम्बाई 1.6m है और इनको A पर कब्जा लगा कर जोड़ा गया है | इन्हें ठीक बीच में 0.5m लम्बी रस्सी DE द्वारा बांधा गया है | सीढ़ी BA के अनुदिश B से 1.2 m की दूरी पर स्थित बिंदु F से 40 kg का एक भार लटकाया गया है | यह मानते हुए की फर्श घर्षण रहित पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए ( $g = 9.8 m / x^{2}$ लीजिए )
संकेत के दोनों और के संतुलन पर अलग अलग विचार कीजिए

Video Solution

Text Solution

Verified by Experts

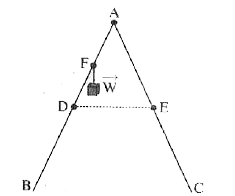
दिया गया है -
AB = AC = 1.6 m
DE = 0.5 m
D तथा E मध्य बिंदु है।
$∴$ AD = DB = AE = EC
$= \frac{1.6}{2} = 0.8$
BF = 1.2 m
AF = 0.4 m
T = रस्सी में तनाव = ?

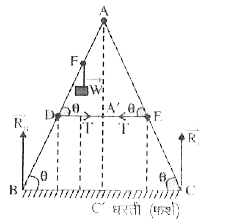
बिंदु B तथा C पर फर्श द्वारा आयतित बल
$R_{B} = R_{C}$ = ?
W = 40 kg भार
$= 40 \times 9.8 N = 392 N$
माना
$∠ A D E = ∠ A E D = θ$
$= ∠ A B C = ∠ A C B$
यहाँ पर A.,DE भुजा का मध्य बिंदु है।
$∴ D A . = \frac{0.5}{2} = 25 m$
$D F . = 0.125 m$
चित्र से यह स्पष्ट है कि
$R_{B} + R_{c} = W = 39.2 N$
विभिन्न बलों के अपूर्ण A के परित लेने पर
$R_{B} = B C . = W \times D F . + T \times A A .$
या $R_{B} \times A B cos θ = W \times 0.125 + T \times 0.8 sin θ$
इसी प्रकार सीढ़ी AC के लिए
$R_{C} = C C . = T \times A A .$
या $R_{C} \times A C cos θ = T \times 0.8 sin θ$
अब $Δ D F F .$ में
$cos θ = \frac{D F .}{D F} = \frac{0.125}{0.4}$
= 0.3125 = cos ${71.8}^{\circ}$
$θ = {71.8}^{\circ}$
$sin 71.8 = 0.9500$
${tan 71.8}^{\circ} = 3.0415$
समीकरण 2 व 4 से
$R_{b} \times 1.6 \times 0.3125 = 392 \times 0.125 + T \times 0.8 \times 0.9500$
इसी प्रकार
$R_{C} = 1.6 \times 0.3125 = T \times 0.8 \times 0.9500$
$0.5 R_{C} = 0.7 6 T$
समीकरण 5 तथा 6 से
$0.5 R_{B} = 49 + 0.5 R_{C}$
या $\frac{1}{2} (R_{B} - R_{C}) = 49$
$R_{B} - R_{C} = 98$
समीकरण 1 तथा 7 को जोड़ने पर $2 R_{B} = 392 + 98 = 490$
$R_{B} = \frac{490}{2} = 245 N$
$∴ R_{C} = R_{B} - 98$
$R_{C} = 245 - 98 = 147$
समीकरण 6 तथा 8 से
$0.5 \times 147 = 0.76 T$
या $T = \frac{0.5 \times 147}{0.76}$
T = 96.7 N = 97N

Updated on:21/07/2023

|

Class 11 PHYSICS CIRCULAR MOTION

Topper's Solved these Questions

Similar Questions

SANJEEV PUBLICATION-कणों के निकाय तथा घूर्णी गति -पाठ्यपुस्तक के प्रश्न

Home
Ask Doubt
Profile