In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔABC
(iv) AQ=CP
(v) APCQ is a parallelogram.
i) In ΔAPD and ΔCQB,
=>AD = CB (Opposite sides)
=>∠ADP = ∠CBQ (Alternate interior angles)
=> DP = BQ (Given)
So,ΔAPD ≅ ΔCQB (by SAS congruence rule)
(ii) Since ΔAPD ≅ ΔCQB,
∴ AP = CQ
(iii) In ΔAQB and ΔCPD,
=>∠ABQ = ∠CDP (Alternate interior angles )
=>BQ = DP (known)
=>AB = CD (Opposite sides )
∴ ΔAQB ≅ ΔCPD (Using SAS congruence rule)
(iv) Since ΔAQB ≅ ΔCPD,
∴ AQ = CP
(v) Using (ii) and (iv)
AQ = CP and AP = CQ
Since opposite sides in quadrilateral APCQ
are equal to each other, thus APCQ is a parallelogram.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - QUADRILATERALSEXERCISE - SOLVED EXAMPLES8videos
QUADRILATERALS
- BOOK - NCERTCHAPTER - QUADRILATERALSEXERCISE - SOLVED EXAMPLES8videos
QUADRILATERALS
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - SOLVED EXAMPLES10videos
PROBABILITY
- BOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 14.12videos
STATISTICS
Similar Questions
In parallelogram ABCD two points P and Q are taken on diagonal BD such that DP = BQ (set figure). Show that:
(i)ΔAPD≅CQB(ii)AP=CQ(iii)ΔAQB≅ΔCPD(iv)AQ=CP(v)APCQis a parallelogram. ltbegt
View SolutionABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that
(i) ΔAPB≅ ΔCQD
(ii) AP = CQ
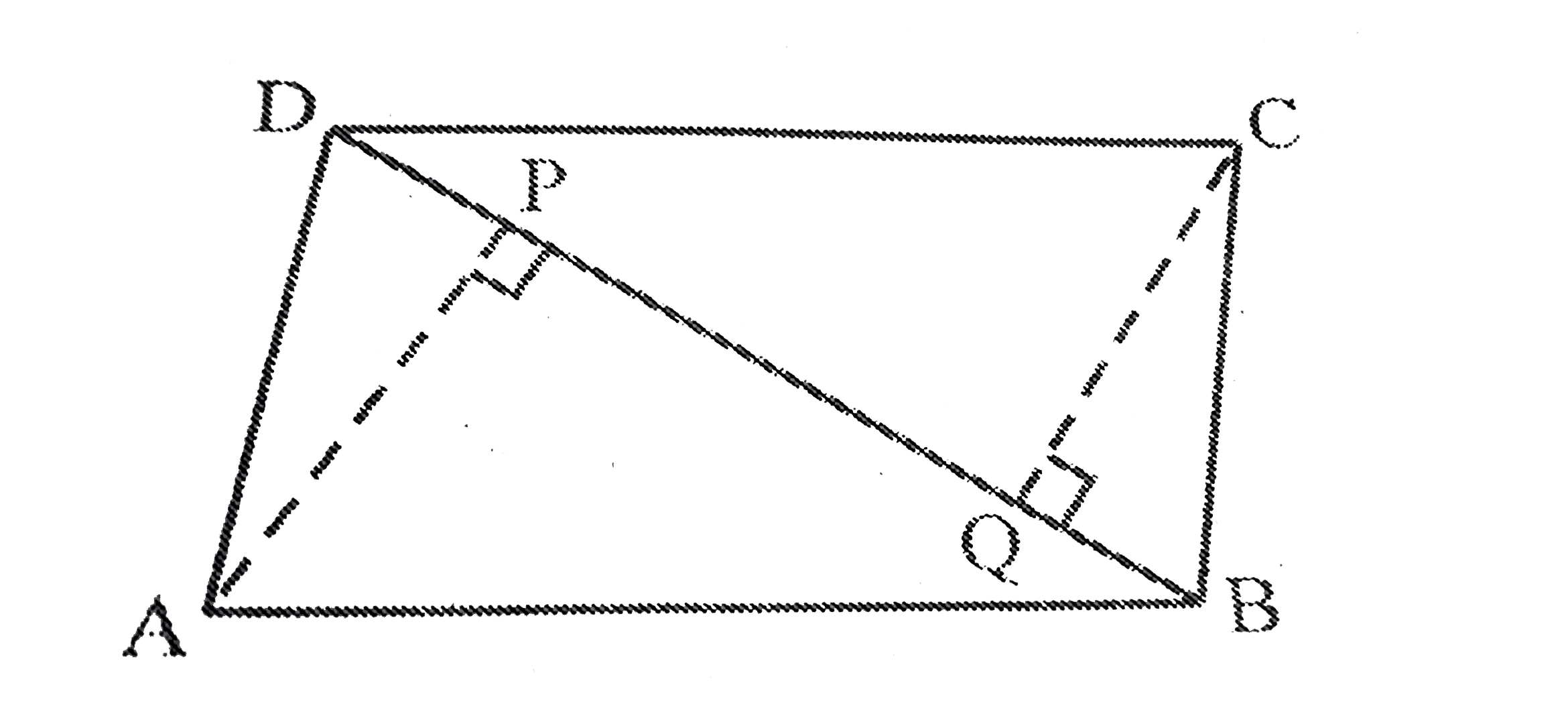View Solution
Knowledge Check
- Question 1 - Select One
ABCD is a parallelogram. P and Q are mid points of BC & CD. Find the area of ΔAPQ if area of ΔABC is 12.
AtrapeziumBparallelogramCsquareDnone of these
In Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP
View SolutionIn Figure altitudes AD and CE of DABC intersect each other at the point P. Show that:
(i) ΔAEP~ΔCDP
(ii) ΔABD~ΔCBE
(iii) ΔAEP~ΔADB
(iv) ΔPDC~ΔBEC
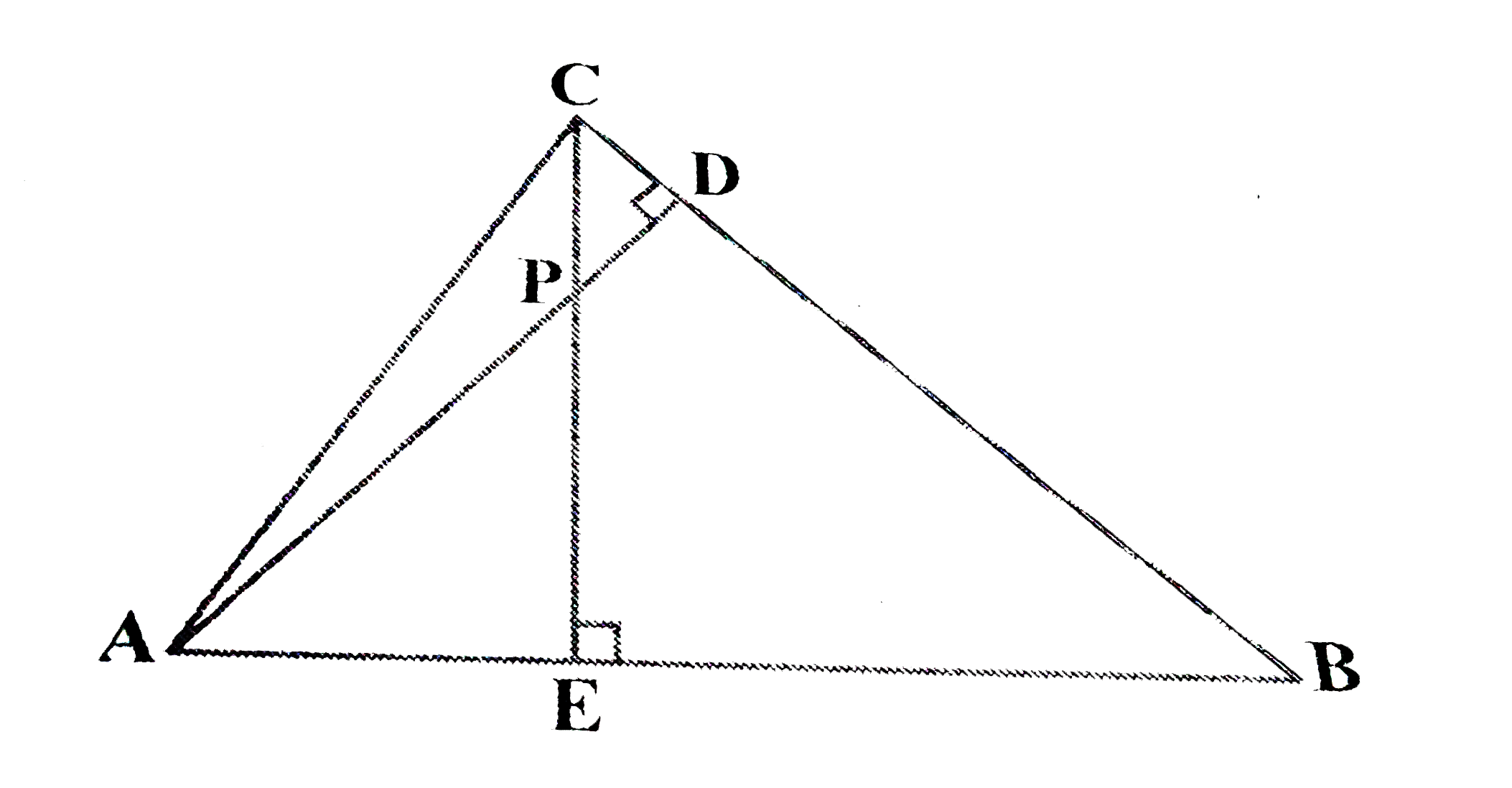View Solutionl and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that ΔABC≅ΔCDA.
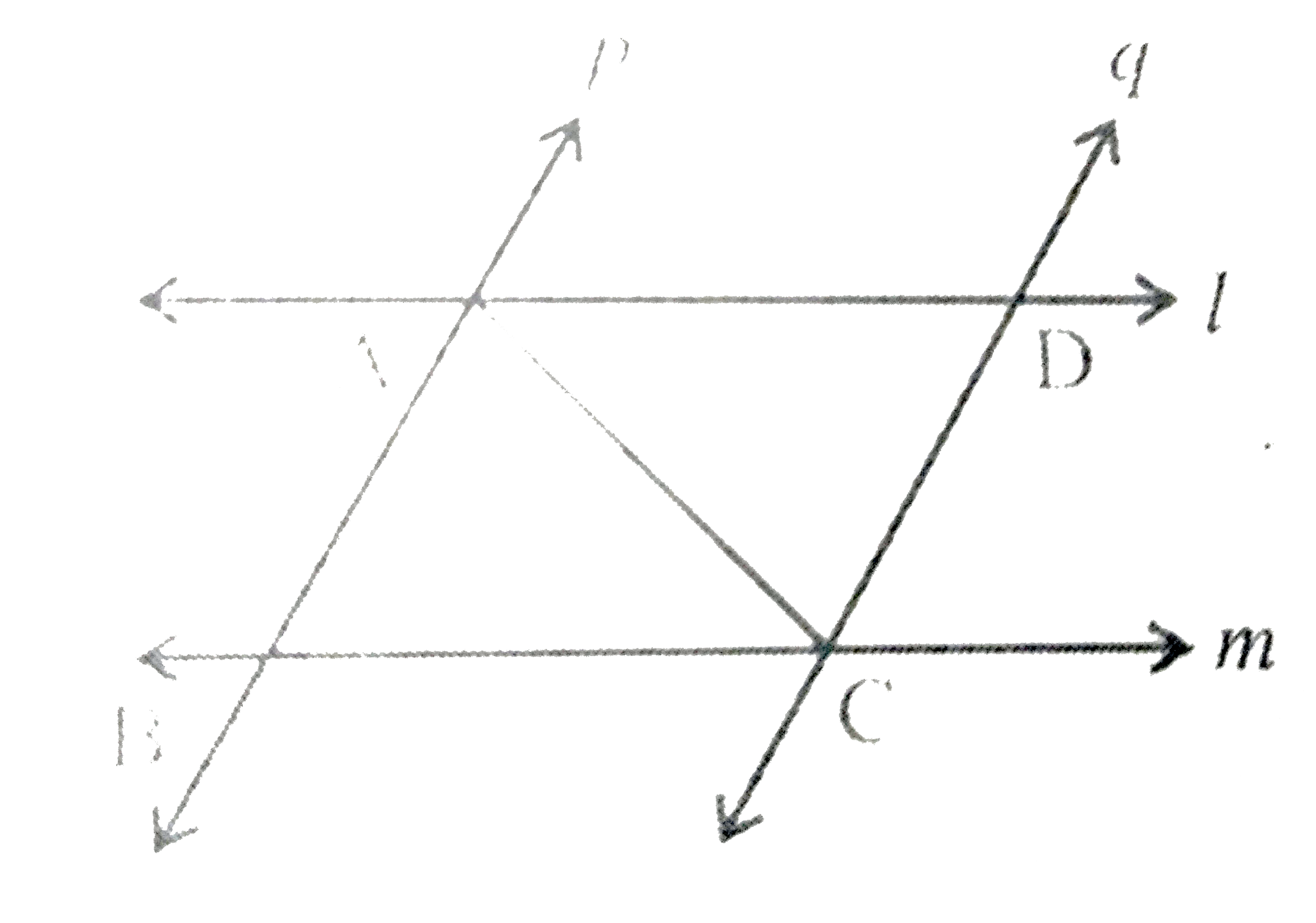View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionABCD is a trapezium in which ABDC . P and Q are points on sides AD and BC such that PQAB . If PD=18 , BQ=35 and QC=15 , find AD .
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionIn Figure, ABCD and PQRC are rectangles and Q is the mid-point of AC . Prove that DP=PC (ii) PR=12 AC
View Solution