A tangential force F acts at the top of a thin spherical shell of mass m and radius R. The acceleration of the shell if it rolls without slipping is

A

$\frac{5 F}{6 m}$

B

$\frac{6 F}{5 m}$

C

$\frac{3 F}{2 m}$

D

$\frac{F}{6 m}$

Text Solution

Verified by Experts

The correct Answer is:B

Torque due to the force F on a thin spherical shell,
$τ = r \times F$
= 2R F sin $90^{\circ}$ = 2F [ $∵ {sin 90}^{\circ}$ = 1 ]
$∵$ Angular acceleration,
$α = \frac{τ}{I}$ …. (i)
Where, I is moment of intertia of a thin spherical shell.
From parallel axes.s theorem, moment of inertia of sphereical shell,
I = $I_{c m} + M r^{2}$
or $I = \frac{2}{3} M R^{2} + M R^{2} (∵ r = R)$
From Eqs . (i) we get
$α = \frac{2 R F}{\frac{2}{3} M R^{2} + M R^{2}}$
$= (\frac{6}{5}) \frac{F}{R M}$
Hence, the tangential acceleration, $a_{τ} = R α$
or $a_{τ} = (\frac{6}{5}) \frac{F}{R M} \times R = \frac{6}{5} \frac{F}{M}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION PAPER 2019

Similar Questions

Knowledge Check

Question 1 - Select One

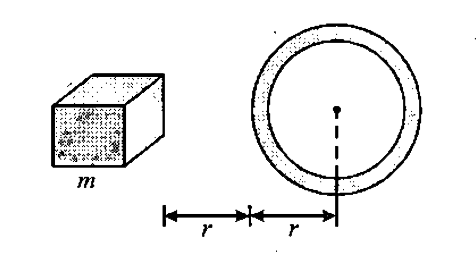
A tangential force $F$ acts at the top of a thin spherical shell of mass $m$ and radius $R$ . Find the acceleration of the shell if it rolls without slipping.
Aa. Acceleration of disc = 2F/3m
Bb. Friction force between disc and surface = 2F/3
Cc. Acceleration of disc = 6F/5m
Dd. Friction force between disc and surface is F/3
Question 2 - Select One
A block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :

AOnly gravitational field inside the shell is zero
BGravitational field and gravitational potential both are zero inside the shell
CGravitational potential as well as gravitational field inside the shell are not zero
DCan't be ascertained.
Question 3 - Select One or More
Consider $a$ thin spherical shell of uniform density of mass $M$ and radius $R$ :
AThe gravitational field inside the shell will be zero
BThe gravitational self energy of shell is $\frac{G M^{2}}{2 R}$
CAttractive force experience by unit area of the shell pull the other half is $\frac{G M^{2}}{2 R^{2}}$
DNet gravitational force with which one hemisphere of the shell arracts other, is $\frac{G M^{2}}{8 R^{2}}$

Recommended Questions

Home
Ask Doubt
Profile