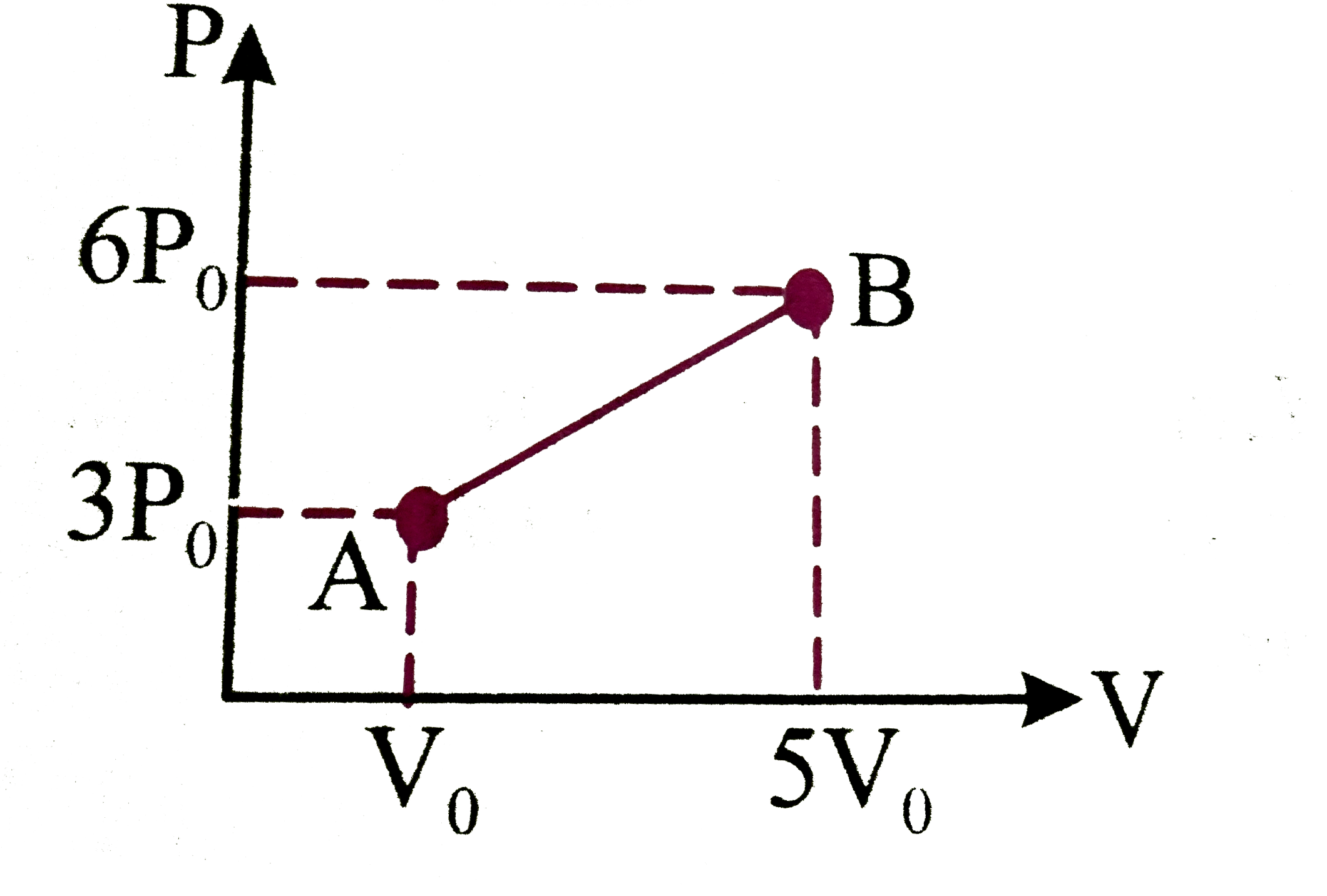
One mole of a monatomic ideal gas undergoes the process A B in the given p-V diagram. Specific heat capacity in the process is

The correct Answer is:B
According to the question,

Now, the termperature at point A and B By, pV = nRT (from ideal gas equation )
Temperature at point A,
Temperature at point B,
So, the termperature difference,
Or,
Now, Due to the adiabatic processs, change is internal energy,
T
or , ....(i)
Work done by the gas undergoes the process
A B
W = Area under p - V graph
or
or ... (ii)
Now, by first law of thermodynamics,
+ W
By putting the values from Eqs. (i) and (ii) to above Eq. we get
or C
or
So, the specific heat capacity in the process A B is C = R .
Similar Questions
Knowledge Check
One mole of a monoatomic ideal gas undergoes process AB in given P – V diagram then average specific heat for this process is:
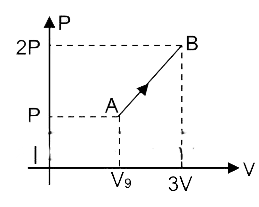 A21R10B18R10C9R10D13R10
A21R10B18R10C9R10D13R10One mole of a monoatomic gas undergoes a linear process A→B in P−v diagram. The volume of the gas when the process turns from an endothermic to an exothermic one is
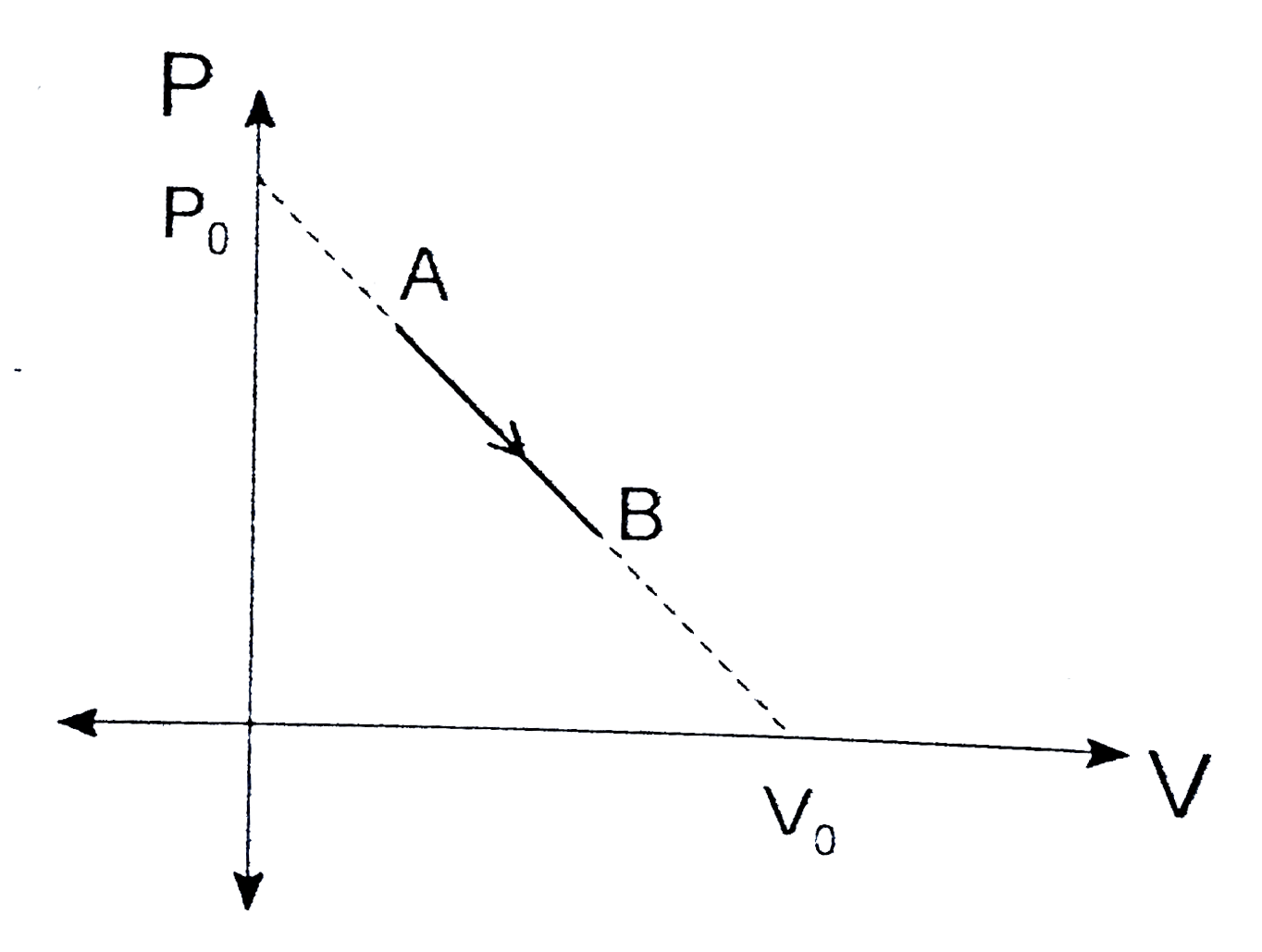 A58v0Bv02C8v015D3v05
A58v0Bv02C8v015D3v05One mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.
R is a gas constant.A3R4BR2CR3D2R3
One mole of a monoatomic ideal gas undergoes the process A→B in the given P-V diagram. What is the specific heat for this process?
View SolutionOne mole of a monoatomic gas undergoes a linear process A→B in P−v diagram. The volume of the gas when the process turns from an endothermic to an exothermic one is

View SolutionOne mole of monatomic ideal gas undergoes the process A→B , as in the given P−V diagram . The specific heat for this process is

View SolutionOne mole of a monatomic ideal gas is taken along the cycle ABCA as shown in the diagram.

The ratio of specific heat in the process CA to the specific heat in the process BC is
View SolutionOne mole of a monatomic ideal gas is taken along the cycle ABCA as shown in the diagram.

The ratio of specific heat in the process CA to the specific heat in the process BC is
View Solution
