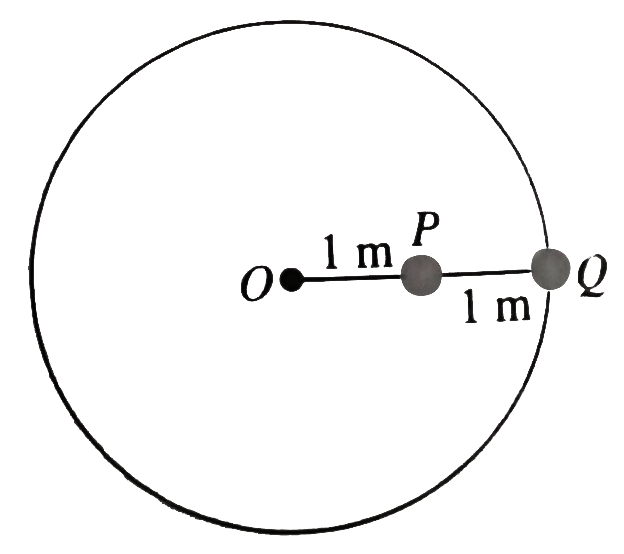
Two spheres P and Q, each of mass 200 g are attached to a string of length one metre as shown in the figure. The string and the spheres are then whirled in a horizontal circle about O at a constant angular speed. The ratio of the tension in the string between P and Q to that of between P and O is (P is at mid-point of the line joining O and Q)

A

$\frac{1}{2}$

B

$\frac{2}{3}$

C

$\frac{3}{2}$

D

$\frac{2}{1}$

Text Solution

Verified by Experts

The correct Answer is:B

Tension between P and Q is $T_{1}$ = centripetal force on $Q = m r ω^{2}$
$= 200 \times 1 \times ω^{2} (g \cdot m \cdot \frac{{rad}^{2}}{s^{2}})$
Tension between O and P is $T_{2}$ = centripetal force on Q+ centripetal force on P $= 200 \times 1 \times ω^{2} + 200 \times \frac{1}{2} \times ω^{2}$
$= 300 \times 1 \times ω^{2} (g \cdot m \cdot \frac{{rad}^{2}}{s^{2}})$
Ratio of tension is
$\frac{T_{1}}{T_{2}} = \frac{200 \times 1 \times ω^{2}}{300 \times 1 \times ω^{2}} = \frac{2}{3}$

|

Updated on:21/07/2023

Class 12 PHYSICS ONLINE QUESTION PAPER 2018

Similar Questions

Knowledge Check

Question 1 - Select One

Two spheres of equal masses are attached to a string of length 2 m as shown in figure. The string and the spheres are then whirled in a horizontal circle about O at a constant rate. What is the value of the ratio:
A $\frac{1}{2}$
B $\frac{2}{3}$
C $\frac{3}{2}$
D2
Question 2 - Select One
A stone of mass 250 gram , attached at the end of a string of length 1.25 m is whirled in a horizontal circle at a speed of 5 m/s . What is the tension in the string ?
A $2.5 N$
B5N
C6N
D8N
Question 3 - Select One
A stone tied to a string of length $l$ is whirled in a horizontal circle at a constant angular speed $ω$ in a circle of radius r. If the string makes an angle $θ$ with vertical then the tension in the string is :
A $m (g cos θ + ω^{2} r)$
B $m \sqrt{ω^{4} r^{2} + g^{2}}$
C $m \sqrt{ω^{2} r^{2} + g^{2}}$
D $m (g cos θ - ω^{2} r)$

Recommended Questions

Home
Ask Doubt
Profile