A ball dropped from a building of height 12 m falls on a slab of 1 m height from the ground and makes a perfect elastic collision.
Later the ball falls on a wooden table of height 0.5 m, makes inelastic collision and falls on the ground. If the coefficient of restitution between the ball and the table is 0.5, then the velocity of the ball while touching the ground is about
(Acceleration due to gravity, $g = 10 m s^{- 2}$ )

A

$15.5 m s^{- 1}$

B

$14.5 m s^{- 1}$

C

$9.2 m s^{- 1}$

D

$8.2 m s^{- 1}$

Text Solution

Verified by Experts

The correct Answer is:D

According to the question,

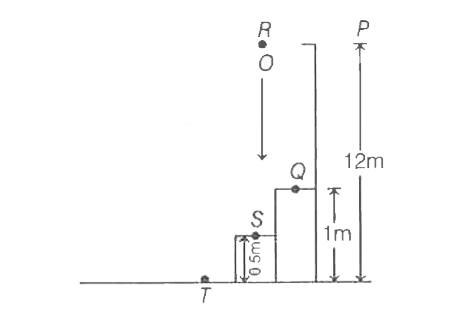
When ball is droped from point P, and collides at point Q, from third equation of the motion,
$v_{Q}^{2} = u^{2} + 2 g h = 0 + 2 \times 10 \times (12 - 1) = 220$
$∴$ Velocity at a point Q, $V_{Q} = \sqrt{220} m / s$
In perfect elastic collision at point Q, there is no loss of kinetic energy.
Hence, the height gain by ball after collision,
$\Rightarrow \frac{1}{2} m v_{Q}^{2} = m g h^{.}$
$\Rightarrow \frac{1}{2} {(\sqrt{220})}^{2} = 10 \times h^{.}$
$\Rightarrow h^{.} = 11 m$
Let velocity of the ball before inelastic collision $= v_{s}$
From energy conservation law,
$\Rightarrow \frac{1}{2} m v_{s}^{2} = m g (11 + 0.5)$
$\Rightarrow v_{s}^{2} = 2 \times 10 \times 11.5$
$\Rightarrow v_{s} = \sqrt{230} m / s$
$∵$ coefficient of restitution, $e = 0.5 = \frac{velocity after collision (v)}{velcoity before collision (v_{s})}$
$\Rightarrow 0.5 = \frac{v}{\sqrt{230}} \Rightarrow v = 0.5 \sqrt{230} m / s$
Again from energy conservation law,
$\frac{1}{2} m v^{2} = m g h . .$
$\Rightarrow \frac{1}{2} {(0.5 \sqrt{230})}^{2} = 10 \times h$
$\Rightarrow h . . = \frac{0.5 \times 230 \times 0.5}{20} = 2.875 m$
Hence, the total height from point T,
$h = h . . + 0.5 = 2.875 + 0.5 = 3.375 m$
From energy conservation law,
$\frac{1}{2} m v_{T}^{2} = m g h$
Velocity of ball while touching the ground,
$v_{T} = \sqrt{2 g h}$
$= \sqrt{2 \times 10 \times 3375}$
$= 8.215 m / s$

Updated on:21/07/2023

|

Class 12 PHYSICS AP EAMCET SOLVED PAPER 2019 (22-04-2019, SHIFT-2)

Topper's Solved these Questions

Similar Questions

Knowledge Check

A ball is dropped from a height of 10 m, as it falls,
Aits velocity increases and acceleration decreases.
Bits velocity decreases and acceleration increases.
Cits velocity increases and acceleration remains constant.
Dits velocity and acceleration remains constant.
A rubber ball is dropped on the ground from a height of 1m. What is the height to which the ball will rebound, if the coefficient of restitution between the ball and the ground is 0.8?
A0.5m
B0.25n
C0.64m
D0.8m
A ball falls from rest from a height h onto a floor, and rebounds to a height $h / 4$ . The coefficient of restitution between the ball and the floor is
A $\frac{1}{\sqrt{2}}$
B $\frac{1}{2}$
C $\frac{1}{4}$
D $\frac{3}{4}$

TS EAMCET PREVIOUS YEAR PAPERS-AP EAMCET SOLVED PAPER 2019 (22-04-2019, SHIFT-2)-PHYSICS

Home
Ask Doubt
Profile