A body is projected vertically upwards from the surface of the earth with a velocity sufficient to carry it to infinity . The time taken by it to reach a height of three times the radius of the earth is ( acceleration due to gravity = 9.8 ms−2and radius of the earth = 6400 km)
44.44 min
22.22 min
18.76 min
37.52 min
The correct Answer is:A
If at a distance r from the centre of the earth the body has velocity ν then by conservation of mechanical energy
(TE)at weight=(TE)at surface
12mv2+(−GMmr)=12mv2e+(−GMmR)
where ve = escape velocity.
v2=v2e+{2GMRv[Rr−√2gRg]=GMR2}
V2=2gR+2gR(Rr−1)
v=√2gR2r,So,v=drdt=R√2gr ⋯(i)
=R√2gr
Intergrating Eq. (i) we get
∫t0dt=1R√2g∫R+hRr1/2.dr
⇒t=231R√2g[(R+h)3/2−R3/2]
t=13
⎷2Rg[(1+hR)3/2−1]
According to equestion h = 3R
t=13
⎷2Rg[(1+3RR)3/2−1]
t=13√2Rg×7
Putting all values we get
t=13(2×6400×1039.8)×7
[∵R=6400×103]
t=803×14.2×7s
t=2666.65s
t= 44.44min
Topper's Solved these Questions
Similar Questions
A body is projected vertically upward from the surface of earth with a velocity sufficient to carry it to initially. Calculate the time taken by it to reach height h.
View SolutionA body is projected vertically upward from the surface of earth with a velocity sufficient to carry it to initially. Calculate the time taken by it to reach height h.
View Solution
Knowledge Check
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A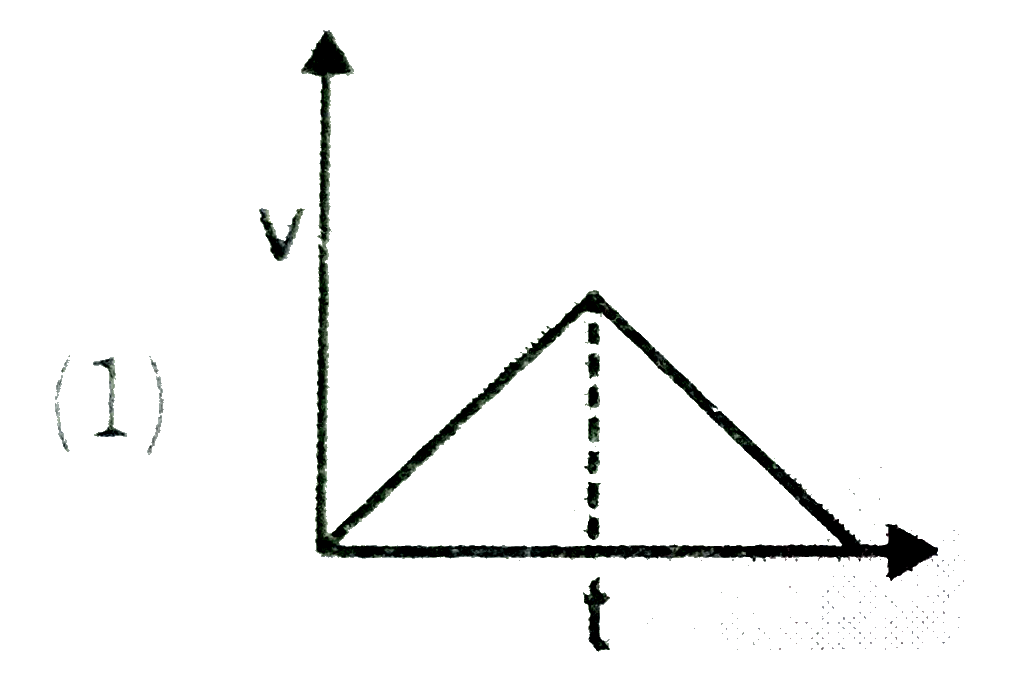 B
B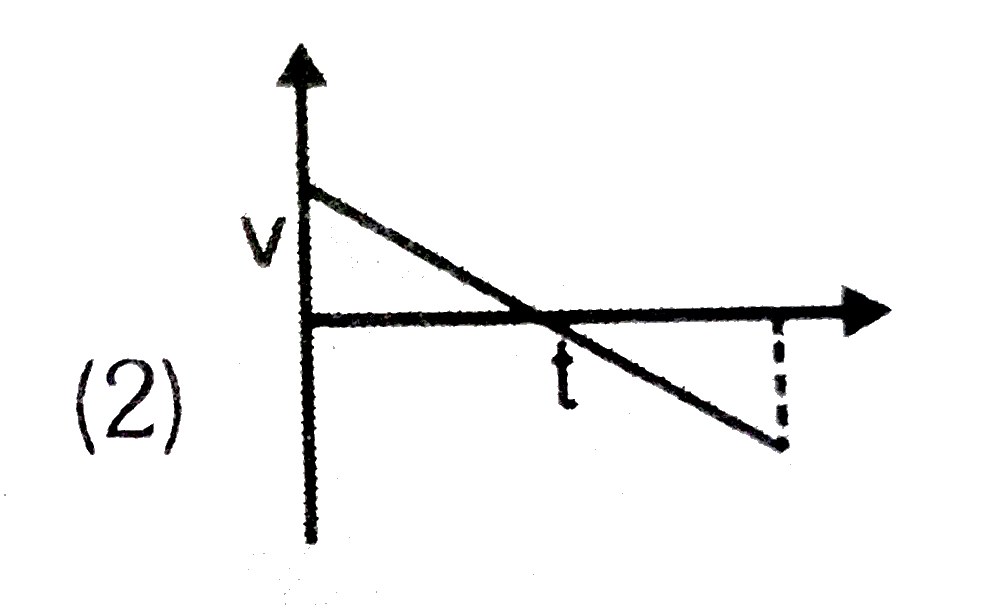 C
C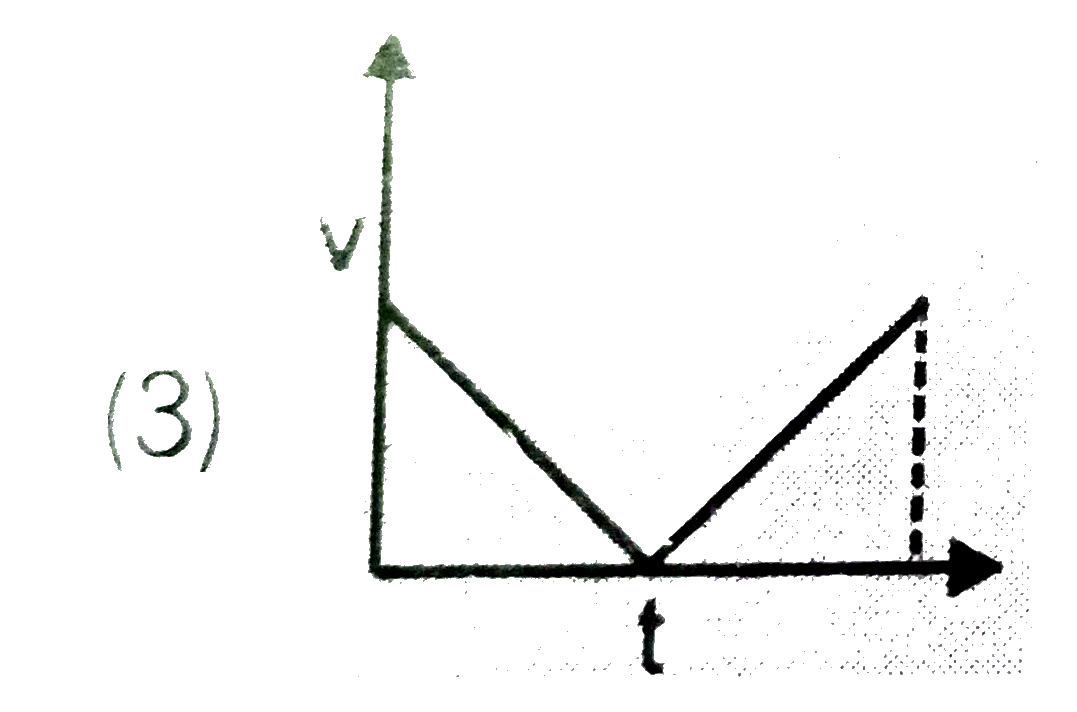 D
D
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
View SolutionA body is projected vertically upward from the surface of the earth with escape velocity. Calculate the time in which it will be at a height (measured from the surface of the arth) 8 time the radius of the earth (R). Acceleration due to gravity on the surface of the earth is g.
View SolutionAt what height from the surface of earth, the acceleration due to gravity decreases by 2% ? [Radius of earth = 6,400 km.]
View SolutionA body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionA body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionCalculate the height at which the value of acceleration due to gravity becomes 50% of that at the earth.
(Radius of the earth = 6400 km)
View SolutionAn object is projected vertically upward from the surface of the earth of mass M with a velocity such that the maximum height reached is eight times the radius R of the earth. Calculate:
(i) the initial speed of projection
(ii) the speed at half the maximum height.
View Solution
