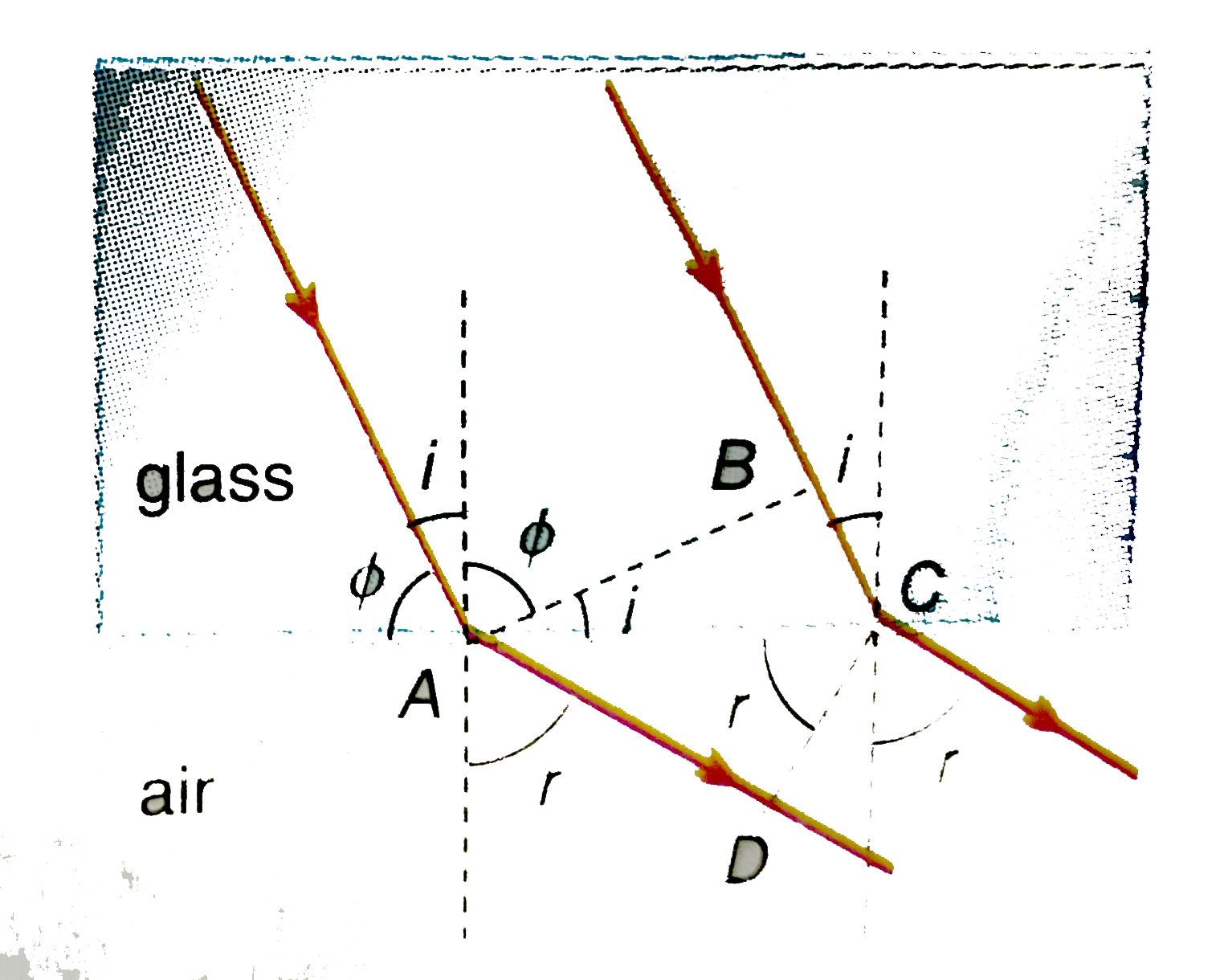
A parallel beam of rays of width 20 cm passing through a glass slab makes an angle with its plane surface. If the beam emerges into air from this surface then calculate the width of emergent beam. Refractive index of glass = 1.8.
The width of the beam of parallel rays = AB = 20 cm and the width of the beam of emergent rays in air = CD.
From Fig. 2.13, I =
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - HIGHER ORDER THINKING SKILL (HOTS QUESTION)
25 Videos
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - SECTION RELATED QUESTION
18 Videos
- REFLECTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE
3 Videos
- SEMICONDUCTORS AND ELECTRONICS BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER
31 Videos
Similar Questions
A beam of parallel rays of width b propagates in glass at an angleθto its plane face .The beam width after it goes over to air through this faceis…….if the refractive index of glass is μ.v
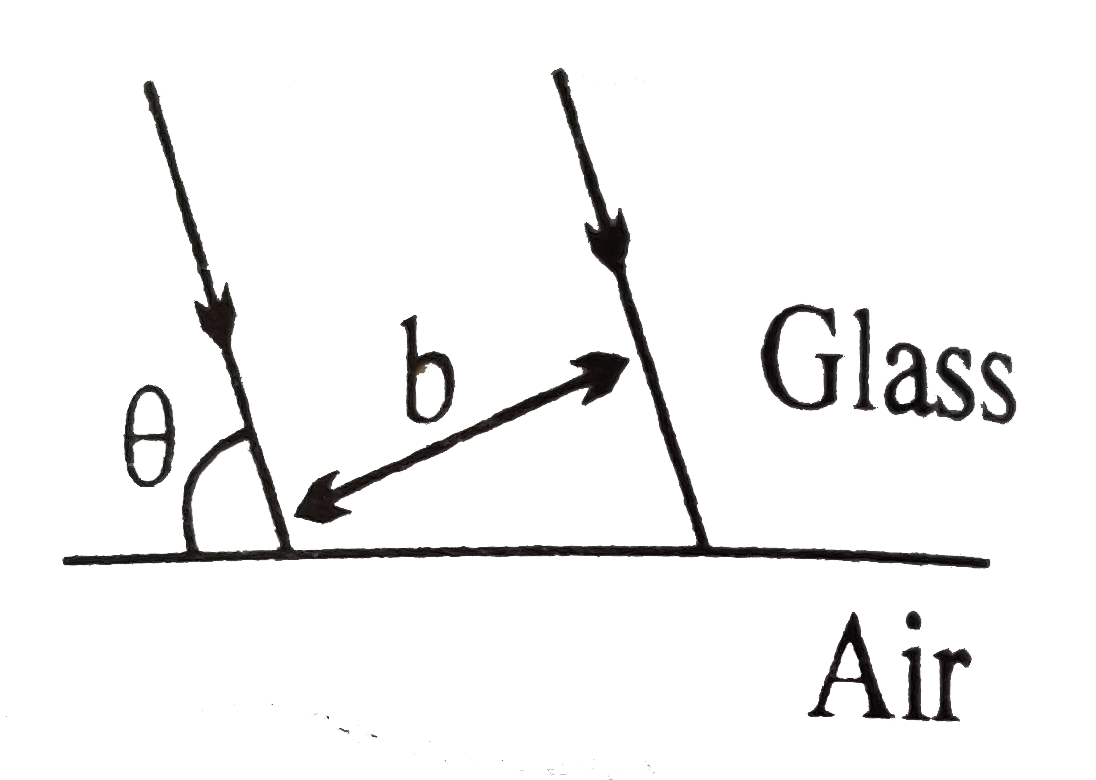
View SolutionA beam of parallel rays of width b cm propagates in glass at an angle θ to its plane face. What would the beam width b1 be after it goes over to air thrugh this face? (The refractive index of the glass is μ)
View Solution
Knowledge Check
A ray of light is incident on a glass slab of refractive index 1.5, making an angle of 40∘ with the surface. The angle of refraction in glass is
A40∘B30∘42'C50∘D60∘A ray of light is incident on a glass slab making an angle of 30∘ with the surface. The angle of refraction in glass, if the refractive index of flass is 1.6 , is
A28∘B33∘C12∘D15∘A beam of light is incident on glass slab making an angle of 60∘ with the surface. The angle of refraction and the velocity of light in glass of R.I. 1.5 are
A19∘28,3×108m/sB29∘28',2×108m/sC19∘28',2×108m/sD29∘28,3×108m/s
A beam of parallel rays of diameter 'b' propagates in glass at an angle θ to its plane. Find the diameter of the beam when it goes to air through this face. (nglass=n)
View SolutionA beam of parallel rays of diameter 'b' propagates in glass at an angle θ to its plane. Find the diameter of the beam when it goes to air through this face. (nglass=n)
View SolutionA parallel beam of monochromatic light is incident on a glass slab at an angle of incidence 60∘. Find the ratio of width of the beam in the glass to that in the air if refractive index of glass is 3/2.
View SolutionThe angle of incidence for a ray of light passing through an equilateral glass prism is equal to its angle of emergence. Also, the angle of emergence is 3/4 times the angle of prism. Calculate the angle of deviation and refractive index of prism's material.
View SolutionA parallel beam of monochromatic light is incident on a glass slab at an angle of 35∘. The ratio of width of beam in glass to that in air is [ μg=1.5]
View Solution
