On placing a transparent glass cube on the printed page of a book, it was found that the covered printed words are not visible from any of the lateral sides of the cube. Explain why?
The refractive index of glass relative to air, μ=1.5.
So the critical angle for the two media,
θc=sin−1(1μ)=sin−1(11.5)
=42∘(nearly)
There is always a thin layer of air between the glass cube and the paper [Fig. 2.79]. If any ray from printed words is incident on the lower surface of the cube even with the maximum angle of 90∘, then it enters glass with a maximum angle of refraction 42∘. Then, the minimum angle of incidence of the ray on the side face of the cube becomes (90∘−42∘)or48∘. A total internal reflection occurs as this angle is greater than the critical angle, and no ray can emerge out of the side face. So, the printed words are not visible to an eye placed outside any of the side faces.

Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - SECTION RELATED QUESTION
18 Videos
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - NCERT TEXTBOOK QUESTION WITH ANSWER HINT
5 Videos
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - CBSE SCANNER
11 Videos
- REFLECTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE
3 Videos
- SEMICONDUCTORS AND ELECTRONICS BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER
31 Videos
Similar Questions
A rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
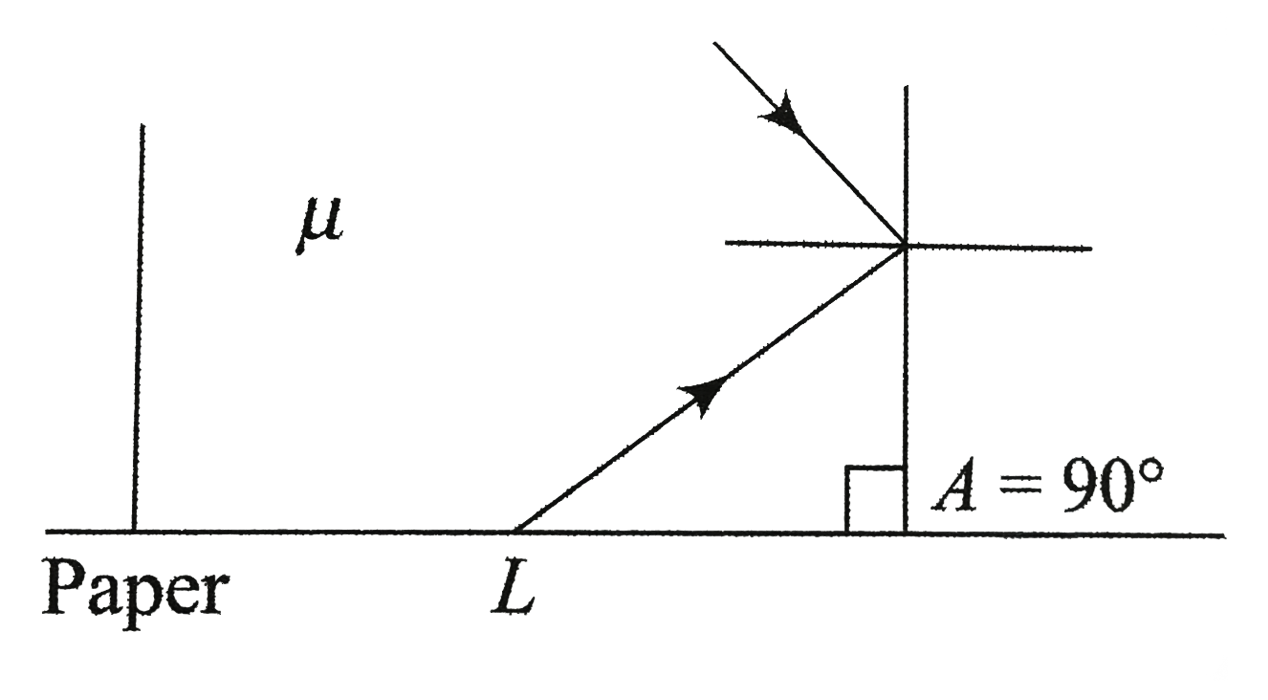
View SolutionA rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.

View Solution
Knowledge Check
Word ‘Newton’s printed on a paper and is placed on a horizontal surface below a cubical glass. The minimum value of refractive index of a cubical glass for which letters are not visible from any vertical faces, of the glass, is (Critical angle =45°)
A√3B0.5C1D√2A charge Q is placed at the centre of a cube of side a. The flux through any one of the sides is :
AQ/ε0BQ/(6ε0)CQ/(4ε0)DQ/(24ε0)A charge Q is placed at the centre of a cube of side a. The flux through any one of the sides is :
AQ/ε0BQ/(6ε0)CQ/(4ε0)DQ/(24ε0)
A glass slab is placed over a page in which letters are printed in different colours. Will the image of all the letters lie in the same plane ?
View SolutionA charge qμC is placed at the centre of a cube of a side 0.1m, then the electric flux diverging from each face of the cube is
View SolutionWhile you are reading a book, you have to move your eyes from word to word, although the full page is in view. Why is it so? Explain.
View SolutionA charge of q μC is placed at the centre of a cube of side 0.1 m. the electric flux diverging from each face of the cube will be
View SolutionA charge qμC is placed at the centre of a cube of a side 0.1m, then the electric flux diverging from each face of the cube is
View Solution
