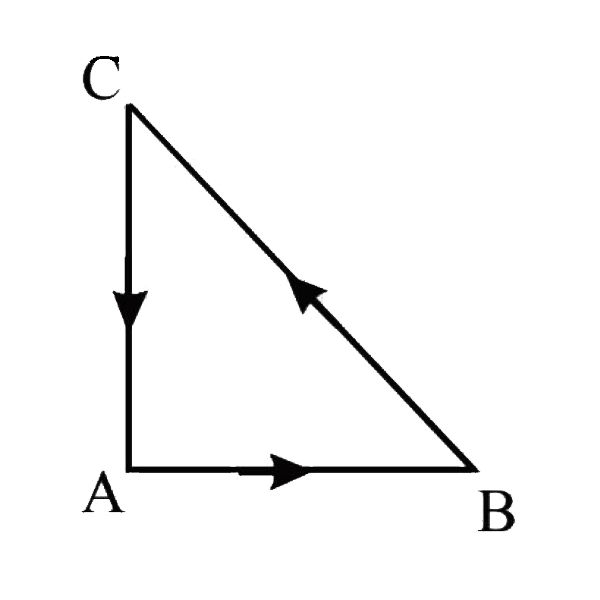
Show that, if three forces acting on a particle can be taken sequentially to form the three sides of a triangle, their resultant is zero.

Text Solution

Verified by Experts

Let $\to a, \to b and \to c$ be the three forces acting at a point O [Fig.2.73 (a)]. Now, taking these forces sequentially and keeping their magnitudes and directions the same, we obtain the three sides of a triangle, $- - \to P Q, - - \to Q R and - - \to R P$ [Fig.2.73(b)].

We have to show that $\to a + \to b + \to c = \to 0$
According to the triangle law of vector addition,
$\to a + \to b = - - \to P R = - - - \to R P or, \to a + \to b = - \to c$
or, $\to a + \to b + \to c = \to 0$
$∴$ The resultant of the forces $\to a, \to b and \to c$ is zero.

Updated on:21/07/2023

Three forces start acting simultaneously on a particle moving with velocity, $¯ v$ . These forces are respresented in magnitude and direction by the three sides of a triangle ABC. The particle will now move with velocity

A(a) less than $\to v$
B(b) greater than $\to v$
C(c) $| v |$ in the direction of the largest force Bc
D(d) $\to v$ , remaining unchanged
The direction of three forces 1N, 2N and 3N acting at a point,are parallel to the sides of an equilateral triangle taken in order. The magnitude of their resultant is:
A $\sqrt{3} N$
B $\frac{\sqrt{3}}{2} N$
C $\frac{3}{2} N$
DZero