A particle is projected from the surface of the earth with a speed of at an angle with the horizontal .
The time of flight of that particle is Solution in Bengali
3 s
4 s
2 s
1 s
The correct Answer is:B
Step by step video, text & image solution for A particle is projected from the surface of the earth with a speed of 20 m* s^(-1) at an angle 30^@ with the horizontal . The time of flight of that particle is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTORBook:CHHAYA PUBLICATIONChapter:VECTORExercise:ENTRANCE CORNER (Integer answer type)
Explore 2 Videos
- VECTORBook:CHHAYA PUBLICATIONChapter:VECTORExercise:EXAMINATION ARCHIVE WITH SOLUTIONS (WBCHSE)
Explore 19 Videos
- VECTORBook:CHHAYA PUBLICATIONChapter:VECTORExercise:ENTRANCE CORNER (Multiple correct answers type)
Explore 11 Videos
- THERMOMETRYBook:CHHAYA PUBLICATIONChapter:THERMOMETRYExercise:EXAMINATION ARCHIEVE - WBJEE
Explore 1 Video
- VISCOSITY AND SURFACE TENSIONBook:CHHAYA PUBLICATIONChapter:VISCOSITY AND SURFACE TENSIONExercise:EXERCISE (CBSE SCANNER)
Explore 9 Videos
Similar Questions
A projectile is launched from the ground and it returns to the ground level. The horizontal range of the projectile is R= 175 m . If the horizontal component of the projectile's velocity at any instant is 25m⋅s−1 , then determine the time of flight of the projectile.
View SolutionThe angle subtended by the vector →A=√3ˆi−ˆj with the y-axis is
View SolutionIn the following figure which of the statements are correct?
View SolutionA scientist proposes a new temperature scale in which the ice point is 25X (X is the new unit of temperature) and the steam point is 305X. The specific heat capacity of water in this new scale is (in J⋅kg−1⋅X−1)
View SolutionState and prove Bernoulli's theorem.
View SolutionA particle is projected at an angle 60∘ with horizontal with a speed v=20m/s. Taking g=10m/s2. Find the time after which the speed of the particle remains half of its initial speed.
View SolutionA particle is projected with a velocity of 30 m//s at an angle 60^(@) above the horizontal on a slope of inclination 30^(@) . Find its range, time of flight and angle of hit.
View SolutionA particle is projected from the ground at an angle of 60∘ with horizontal at speed u=20m/s. The radius of curvature of the path of the particle, when its velocity. makes an angle of 30∘ with horizontal is :
(g=10m/s2
View SolutionA particle is projected at an angle of 60∘ above the horizontal with a speed of 10m/s. After some time the direction of its velocity makes an angle of 30∘ above the horizontal. The speed of the particle at this instant is s
View SolutionA particle is projected from horizontal ground at angle 'θ' with speed 'u'. In same plane of motion a horizontal acceleration 'a' exists so that projected particle returns back to point of projection. Find time of flight.
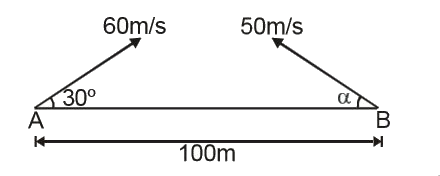
View SolutionA particle A is projected with an initial velocity of 60 m/s. at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a) the angle of projection ∝ of particle B,
View SolutionA particle is projected with a velocity of 20 m/s at an angle of 30^(@) to an inclined plane of inclination 30^(@) to the horizontal. The particle hits the inclined plane at an angle 30^(@) , during its journey. The time of flight is -
View SolutionA particle is projected from a point on the ground surface at different angles keeping the speed of projection as constant range obtained is plotted as function of the angle of projection with the horizontal 'O'. Find the range obtained if particle is projected at angle 30° with the horizontal : 2 g 10 m/s 250m R
View SolutionA particle is projected from the surface of the earth with a speed of 20 m* s^(-1) at an angle 30^@ with the horizontal . The range of that particle is
View SolutionA particle is projected from the surface of the earth with a speed of 20 m* s^(-1) at an angle 30^@ with the horizontal . The maximum height the particle can reach is
View Solution
