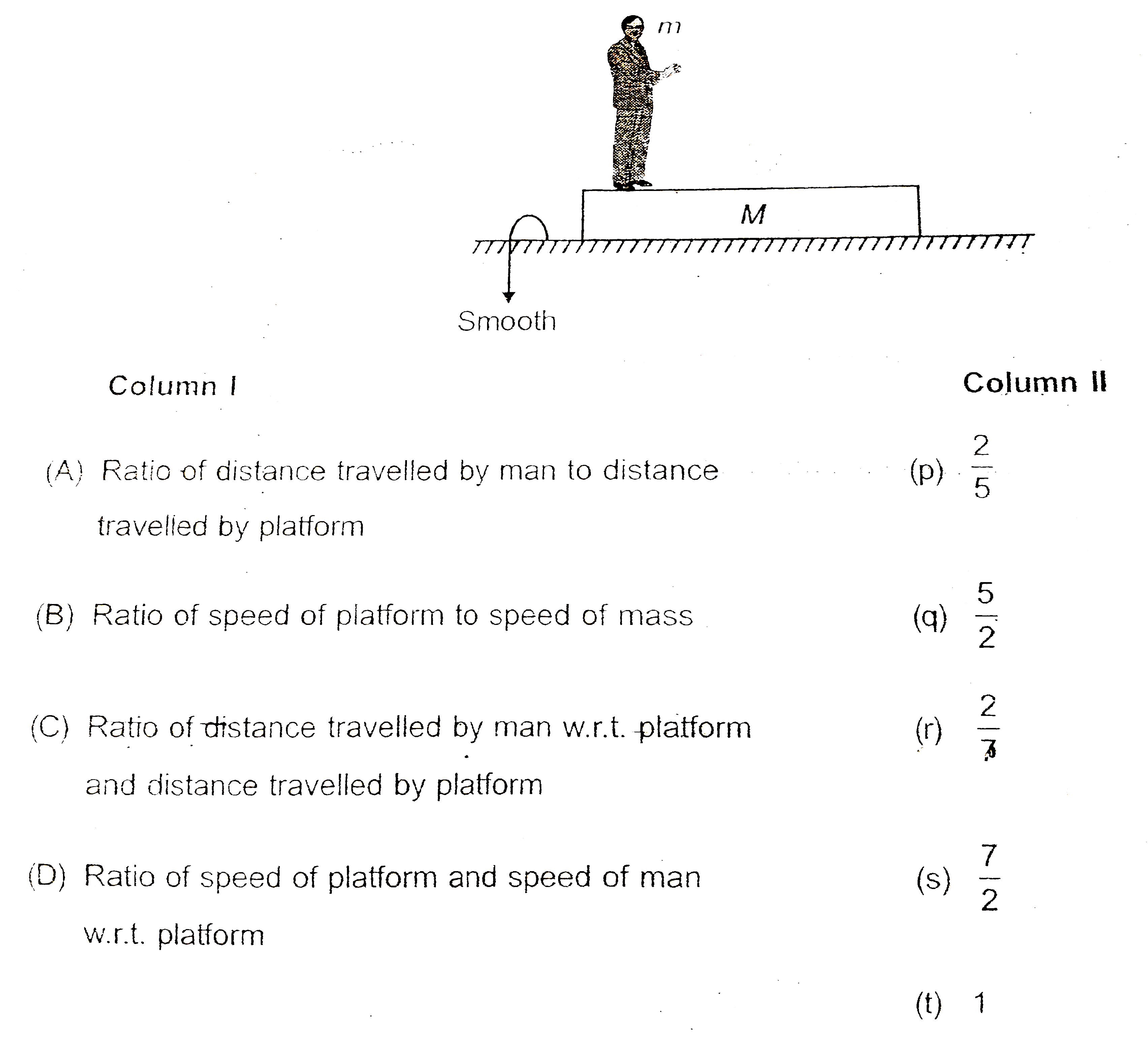A body of mass m is placed on a platform of mass M ( $m < M$ ), moving with a velocity v. If the coefficient of friction between the platform and the mass is $μ$ then for how long will the body continue to slide on the platform and what distance will it cover during that time?

Text Solution

Verified by Experts

When the platform moves the body on it tends to slide backwards. So the frictional force on the body acts in the direction of motion of the platform. It is given by , f = $μ$ mg.
$∴$ Its acceleration a = $\frac{f}{m} = μ g$
When the velocity of the body becomes v it no longer slides over the platform.
We know v = u+at $or, t = \frac{v + u}{a}$
Here u=0, a = $μ g ∴ t = \frac{v}{μ g}$
Again $v^{2} = u^{2} + 2 a s or, s = \frac{v^{2} - u^{2}}{2 a} = \frac{v^{2}}{2 μ g}$
$∴$ The body will slide for a time of $\frac{v}{μ g}$ , and in this interval of time it will cover a distance of $\frac{v^{2}}{2 μ g} .$

Updated on:21/07/2023

A block of mass m is placed gently onto a long plank of mass M moving with a velocity $v_{0}$ on a smooth horizontal floor. If friction is present between M and m :

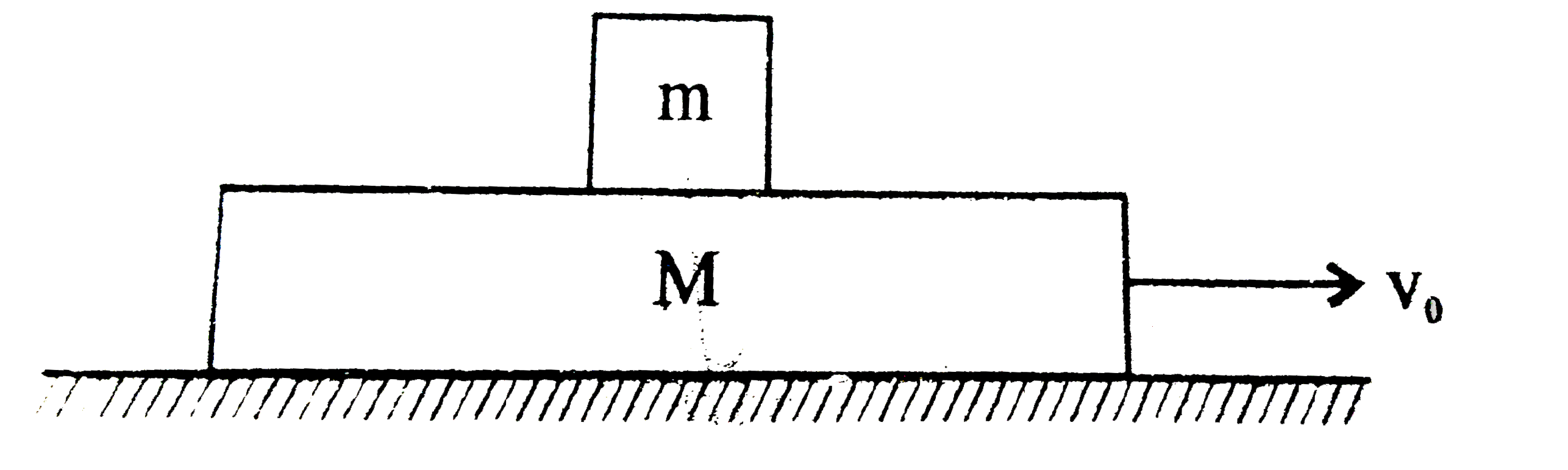A $v_{centre of mass} = \frac{M v_{0}}{M + m}$
B $W_{friction}$ on m is positive
C $W_{Friction}$ on M is negative
Dfinal velocity of both $= \frac{m v_{0}}{m + M}$
A body of mass m kept on the floor of a lift moving downwards is pulled horizontally. If $μ$ is the coefficient of friction between the surface in contact, then
Africtional resistance offered by the floor is 2 $μ m g$ , when lift moves up with a uniform velocity of 5 m/s.
Brictional resistance offered by the floor is $μ u m g$ , when lift moves lift moves up with uniform velocity of 3 m/s.
Cfrictional resistance offered by the floor is $4.8 μ m g$ , when lift accelerates down with an acceleration of $4.8 m / s^{2}$
Dfrictional resistance offered by the floor must lie in the range $0 \leq f < \infty$
If $μ$ is the coefficient of friction between the tyres and road then the least stopping distance for a car of mass m moving with velocity v is
A $v^{2} / 2 μ g$
B $v / 2 μ g$
C $2 v / μ^{2} g$
D $2 v / μ g$