A funnel is rotating around its vertical axis with a constant frequency ν rev/s. A small cube of mass m is placed on the inside wall of the funnel carefully. The wall of the funnely makes an angle θ with the horizontal. If μ is the coefficient of friction between the funnel and the cube, r is the distance between the centre of mass of the cube and the rotational axis, then find the maximum and minimum value of ν for which the cube remains static with respect to the funnel.

Frequency of rotation of the funnel = v rev/s.
Centripetal force required for the cube of mass m to rotate around the circular path of radius r is,
Fr=mω2r=m(2πv)2r=4π2v2mr
Let the block slide down the wall of the funnel when the funnel is at rest. Suppose, V1 is the minimum value of frequency for which the block remains static. At that time. the direction of the frictional force will be upward along the walls of the funnel.
Balancing the forces on the cube, we get
mg = (ncosθ+fsinθ) [ n = normal reaction,
f = limiting value of the static friction ]
= n cos θ+μn sinθ
= n(cosθ+μsinθ) ...(1)
and mω21r=nsinθ−fcosθ=nsinθ−μncosθ
= n(sinθ−μcosθ) ...(2)
From equations (1) and (2) we have,
ω21rg=sinθ−μcosθcosθ+μsinθ
or, (2πv1)2=gr(sinθ−μcosθcosθ+μsinθ)
or, v1=12π√gr(sinθ−μcosθcosθ+μsinθ)
Now, let ν2 be the maximum value of frequency of rotation for which the cube remains static with respect to the funnel. Then the direction of the frictional forces will be downward along the walls of the funnel.
Balancing the forces on the cube, we get
mg = n conθ−fsinθ=n(cosθ−μsinθ) ...(3)
and mω22r=n(sinθ+μcosθ) ...(4)
From equations (3) and (4) we get,
ω22rg=sinθ+μcosθcosθ−μsinθ
or, ν2=12π√gr(sinθ+μcosθcosθ−μsinθ)


Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS )
25 Videos
- CIRCULAR MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
35 Videos
- CIRCULAR MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - SECTION RELATED QUESTIONS
15 Videos
- CALORIMETRYBOOK - CHHAYA PUBLICATIONCHAPTER - CALORIMETRYEXERCISE - EXAMINATION ARCHIVE
5 Videos
- DOPPLER EFFECT IN SOUND BOOK - CHHAYA PUBLICATIONCHAPTER - DOPPLER EFFECT IN SOUND EXERCISE - CBSE SCANNER
2 Videos
Similar Questions
A very small cube of mass m is placed on the inside of a conial funnelof semivertical angle (π/2−θ). The funnel is then set in rotation. If the coefficient of static friction between the cube and the funnel is μ and the centre of the cube is at a distancer from the axis of rotation, what are the largest and smallest angular velocities with which the funnel can be rotated so that the block will not move with respect to the funnel ?
View SolutionA block of mass m kg is pushed up against a wall by a force P That makes an angle 'theta' with the horizontal as shown in The coefficient of static friction between the block and the wall is μ The minimum value of P that allows the block to remain stationary is .
View Solution
Knowledge Check
A block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
Amg cos θBmgCmg sin θDNone of theseA cube of mass m is placed on top of a wedge of mass 2m, as shown in figure. There is no friction between the cube and the wedge. The minimum co - efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is
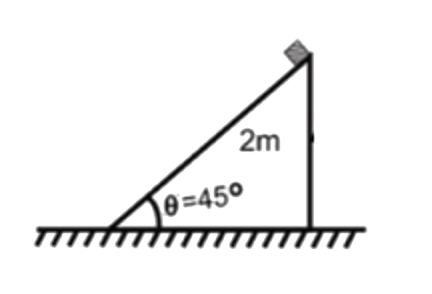 A0.1B0.2C0.3D1√2
A0.1B0.2C0.3D1√2In the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle θ with the horizontal floor. The coefficient of friction between the wall and the ladder is μ1 and that between the floor and the ladder is μ2. the normal reaction of the wall on the ladder is N1 and that of the floor is N2. if the ladder is about to slip. than
 Aμ1=0,μ2≠andN2tanθ=mg2Bμ1≠0,μ2=0andN1tanθ=mg2Cμ1≠0,μ2≠0andN2=mg1+μ1μ2Dμ1=0,μ2≠0andN1tanθ=mg2
Aμ1=0,μ2≠andN2tanθ=mg2Bμ1≠0,μ2=0andN1tanθ=mg2Cμ1≠0,μ2≠0andN2=mg1+μ1μ2Dμ1=0,μ2≠0andN1tanθ=mg2
A block of mass m kg is pushed up against a wall by a force P that makes an angle 'θ' with the horizontal as shown in figure . The coefficient of static friction between the block and the wall is μ . Find the minimum value of P that allows the block to remain stationary .
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass m kg is pushed up against a wall by a force P that makes an angle 'θ' with the horizontal as shown in figure. The coefficient of static friction between the block and the wall is μ. The minimum value of P that allows the block to remain stationary is
View SolutionA cube of mass m is placed on top of a wedge of mass 2m, as shown in figure. There is no friction between the cube and the wedge. The minimum co - efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is

View SolutionIn the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle θ with the horizontal floor. The coefficient of friction between the wall and the ladder is μ1 and that between the floor and the ladder is μ2. the normal reaction of the wall on the ladder is N1 and that of the floor is N2. if the ladder is about to slip. than

View Solution
