Derive an expression for the acceleration of a body of mass m moving with a uniform speed v in circular path of radius r.

Text Solution

Verified by Experts

Let A = initial position of the body ,
B = position of the body after a small time interval t.
So, the angular displacement $θ = ∠ A O B$ , is also small, and the displacement x effectively coincides with the arc AB of the circular path. Then,
Now at A, the velocity v is horizontal , at B, the velocity makes the same angle $θ$ with the horizontal direction, keeping its magnitude v to be the same, as the body moves with a uniform speed v . Again, as $θ$ is small, the change of velocity u, effectively coincides with a circular arc.
So, $θ = \frac{u}{v}$
Then we get, $\frac{x}{r} = \frac{u}{v}$
or, u = $\frac{v}{r} x$
Hence, the acceleration is,
a = $\frac{change of velocity}{time} = \frac{u}{t} = \frac{v x}{r t}$
= $\frac{v}{r} v = \frac{v^{2}}{r}$
also shows that, as $θ$ is small, u is normal to the velocity v. As v is tangential at every point on the circular path, the acceleration a is radial. This is centripetal acceleration of a uniform circular motion.

Updated on:21/07/2023

Figure below shows a body of mass $M$ moving with the uniform speed on a circular path of radius, $R$ . What is the change in acceleration in going from $P_{1}$ to $P_{2}$

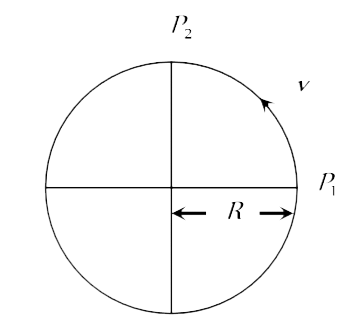AZero
B $v^{2} / 2 R$
C $2 v^{2} / R$
D $\frac{v^{2}}{R} \times \sqrt{2}$
The acceleration of an object moving in a circle of radius R with uniform speed v is
A $\frac{v^{2}}{R}$
B $\frac{v^{2}}{2 R}$
C $\frac{2 v^{2}}{R}$
D $\frac{3 v^{2}}{2 R}$
Figure shows a body of mass m moving with a uniform speed v along a circle of radius r . The change in velocity in going from A to B is

A $v \sqrt{2}$
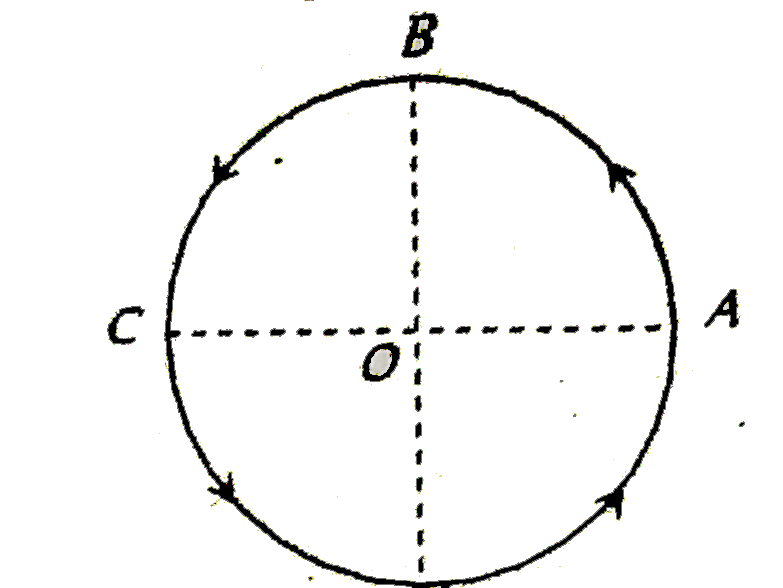B $v / \sqrt{2}$
Cv
DZero