A spaceship while flyting in space, splits up into three equal parts, due to an explosion. One fragment keeps moving in the same direction, the other two fly of at $60^{\circ}$ to the original direction , on either side. If the energy released due to the explosion is twice the kinetic energy of the spaceship, find the kinetic energy of each of the fragment.

Text Solution

Verified by Experts

Let the mass of the spaceship be 3m and initial speed be u.
Hence, mass of each fragment =m . Let their velocity be $v_{1}, v_{2} and v_{3}$ after the explosion [Fig.1.46].

Applying the conservation of momentum law along the direction perpendicular to the original direction of motion,
$0 = m v_{2} {sin 60}^{\circ} = m v_{3} {sin 60}^{\circ}$
$or, m v_{2} {sin 60}^{\circ} = m v_{3} {sin 60}^{\circ}$
$or, v_{2} = v_{3} = v$ (say)
Applying the law of conservation of linear momentum along the original direction of motion ,
$3 μ = m v_{1} + 2 m v {cos 60}^{\circ}$
$or, 3 u = v_{1} + v$
Kinetic energy of the spaceship before explosion
$E = \frac{1}{2} \times 3 μ^{2}$
Energy released during the explosion,
$E_{r} = \frac{1}{2} m (v_{1}^{2} + 2 v^{2}) - \frac{1}{2} \cdot 3 μ^{2}$
According to the problem,
$E_{r} = 2 E or, \frac{1}{2} m (v_{1}^{2} + 2 v_{^} 2) - \frac{1}{2} \cdot 3 μ^{2} = 2 \times \frac{1}{2} \cdot 3 μ^{2}$
$or, v_{1}^{2} + 2 v^{2} - 3 u^{2} = 6 u^{2}$
$or, v_{1}^{2} + 2 v^{2} = 9 u^{2}$ ......(2)
Solving (1) and (2) , $v_{1} = u and v = 2 u$
Hence, kinetic energy of the first fragment after explosion
$= \frac{1}{2} m v_{1}^{2} = \frac{1}{2} μ_{2} = \frac{1}{2} \cdot \frac{2}{3} \cdot E = \frac{1}{3} E$
Kinetic energy of each of the other two fragement
$= \frac{1}{2} m v^{2} = \frac{1}{2} m {(2 u)}^{2} = 2 μ^{2} = 2 \cdot \frac{2}{3} E = \frac{4}{3} E$

A body kept at rest explodes in four identical fragments and it is found that three of them move along mutually perpendicular directions with same kinetic energy K . Total energy released in the explosion is
A3k
B4K
C6K
D8K
An object of mass 3 kg at rest in space suddenly explodes into three parts of the same mass. The momenta of the two parts are $4 ˆ i$ and $2 ˆ j$ respectively. Then the energy released in the explosion is
A60 J
B40 J
C20 J
D10 J
A particle of mass 4m which is at rest explodes into four equal fragments. All 4 fragments are scattered in the same horizontal plane. Three fragments are found to move with velocity V each as shown in the figure. The total energy released in the process of explosion is

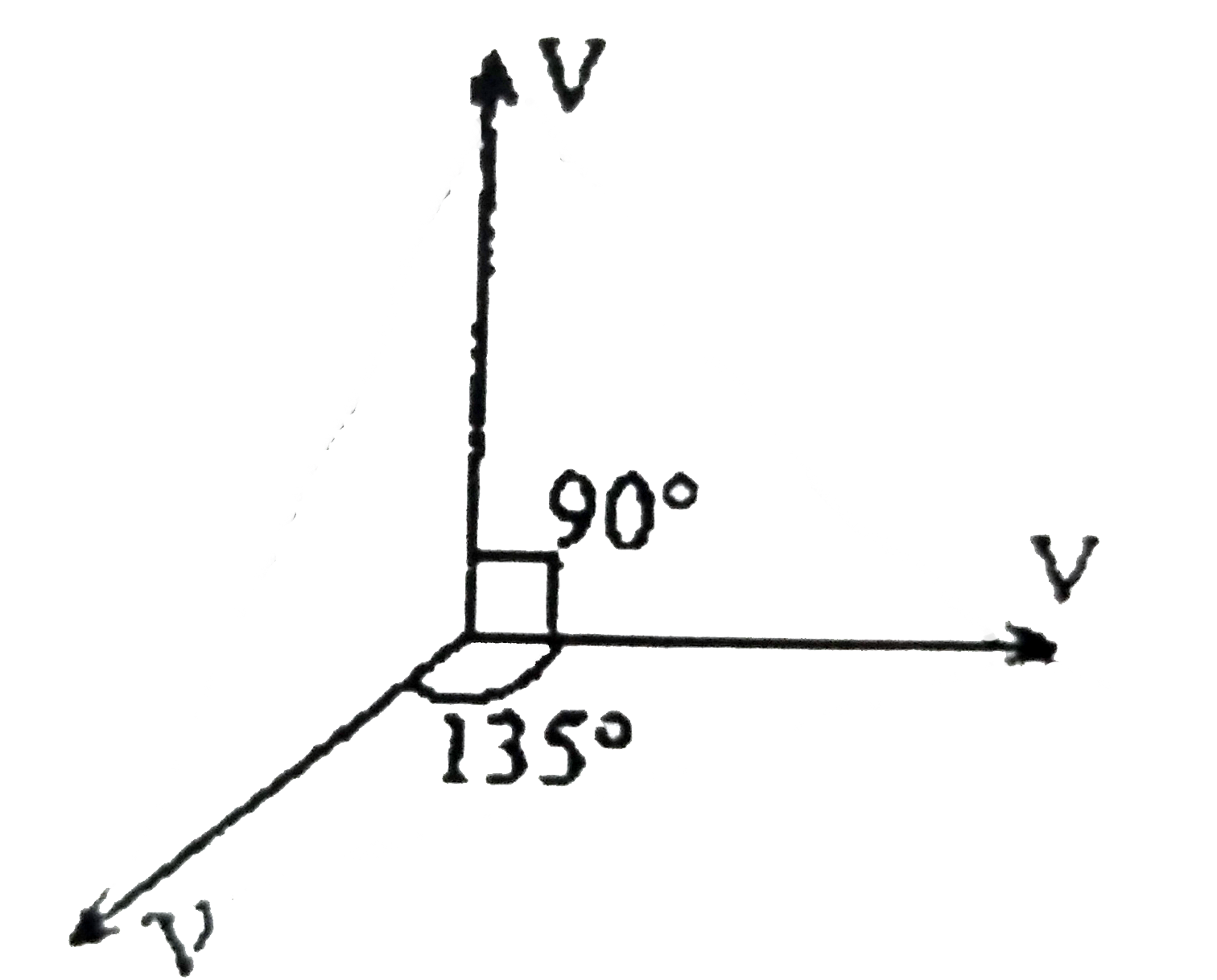A $m V^{2} (3 - \sqrt{2})$
B $m v^{2} (3 - \sqrt{2}) / 2$
C $2 m V^{2}$
D $m V^{2} (1 + \sqrt{2}) / 2$