Three force F,F and √2 F acting at a point are in equilibrium. Find the angles between the forces.
Fig. shows the three force. Let the angles between the forces be α,β and γ, as shown in the figure.
∴ α+β+γ=360∘
or, β+γ=360∘−α
∴ sin(β+γ)=−sinα
By Lami.s theorem,
√2Fsinα=Fsinβ=Fsinγ
∴ β=γ
Also, Fsinβ=√2Fsinαor,sinα=√2sinβ.
Now, sinα=−sin(β+γ)=−sin2β=−2sinβcosβ
Hence, −2sinβcosβ=√2sinβ
or, cosβ=−1√2=cos135∘
∴ β=135∘=γ
and a=360∘−(135∘+135∘)=90∘.

Topper's Solved these Questions
- STATICSBook:CHHAYA PUBLICATIONChapter:STATICSExercise:HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
Explore 18 Videos
- STATICSBook:CHHAYA PUBLICATIONChapter:STATICSExercise:EXERCISE (Multiple Choice Questions )
Explore 14 Videos
- SIMPLE HARMONIC MOTIONBook:CHHAYA PUBLICATIONChapter:SIMPLE HARMONIC MOTIONExercise:CBSE SCANNER
Explore 16 Videos
- SUPERPOSITION OF WAVESBook:CHHAYA PUBLICATIONChapter:SUPERPOSITION OF WAVESExercise:CBSE Scanner
Explore 14 Videos
Similar Questions
PQR is a rigid equilateral triangle frame of a side length L. Forces F1,F2 and F3 are acting along PQ,QR,PR. If the system is in rotational equilibrium find the relation between the forces.
View SolutionFig shows three forces F1,F2 and F3 acting on a rod pivoted at its end. Find the torque of each force about pivot.
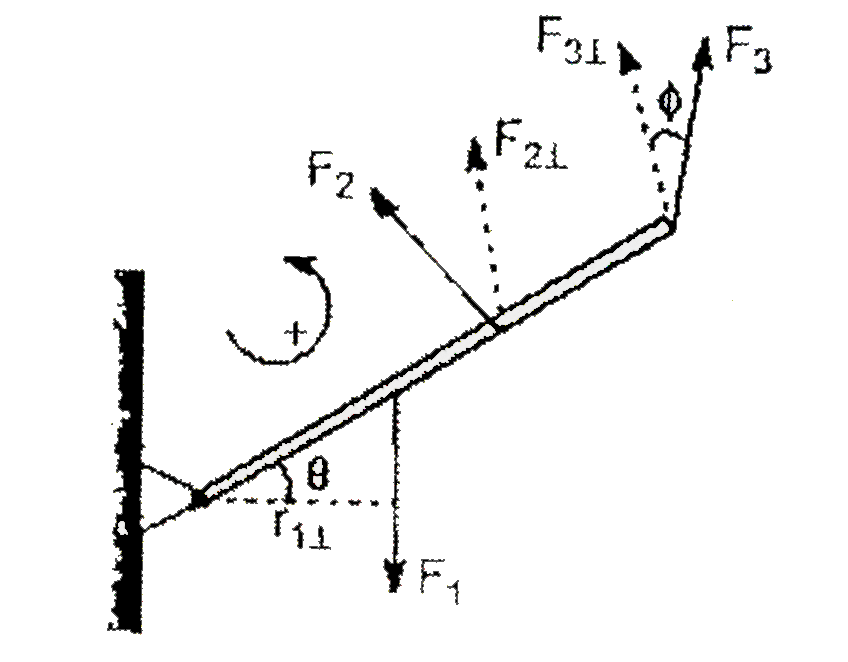
View Solution
Knowledge Check
Three forces of magnitude 30, 60 and P acting at a point are in equilibrium. If the angle between the first two is 60∘, the value of P is
A30√7B30√3C20√6D25√2Three forces of magnitude 30, 60 and P acting at a point are in equilibrium. If the angle between the first two is 60∘, the value of P is
A30√7B30√3C20√6D25√2Three forces 9,12 and 15N acting at a point are in equilibrium . The angle between 9N and 15N is
Acos−1(3/5)Bcos−1(4/5)Cπ−cos−1(3/5)Dπ−cos−1(4/5)
Two force F1 and F2 are acting on a body. One force is double that of the other force and the resultant is equal to the greater force. Then the angle between the two forces is :-
View SolutionTwo forces F1 and F2 are acting on a body. One force is double that of the other force and the resultant is equal to the greater force. Then the angle between the two forces is
View SolutionTwo forces F1 and F2 are acting on a body. One force is double that of the other force and the resultant is equal to the greater force. Then the angle between the two forces is
View SolutionTwo force F1 and F2 are acting on a body. One force is double that of the other force and the resultant is equal to the greater force. Then the angle between the two forces is :-
View SolutionTwo forces of equal magnitude F are at a point. If θ is the angle between two forces then magnitude of the resultant forces will be
View Solution
