Four identical bricks are kept one over another in such a way that a part of each brick is projected out of the brick below it. For equilibrium of the system, how much of the three upper bricks can be extended out?
12 of the topmost, 14 th of the second one and 16 th of the third
Topper's Solved these Questions
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - ENTRANCE CORNER ( Assertion-reason type )
5 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - ENTRANCE CORNER ( Multiple correct answers type )
1 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - Hots Numerical Problems ( Based on Centre of Gravity )
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - CBSE Scanner
14 Videos
Similar Questions
Infinite number of bricks are placed one over the other as shown in the figure. Each succeeding brick having half the length and breadth of its preceding brick and the mass of each succeeding bricks being (1/4)th of the preceding one. Taking 'O' as the origin, the x coordinate of centre of mass of the system of bricks is at

View SolutionTwo identical bricks of length L are piled one on top of the other on a table as shown in the figure the maximum distance S the top brick can overhand the table with the system still balanced is:
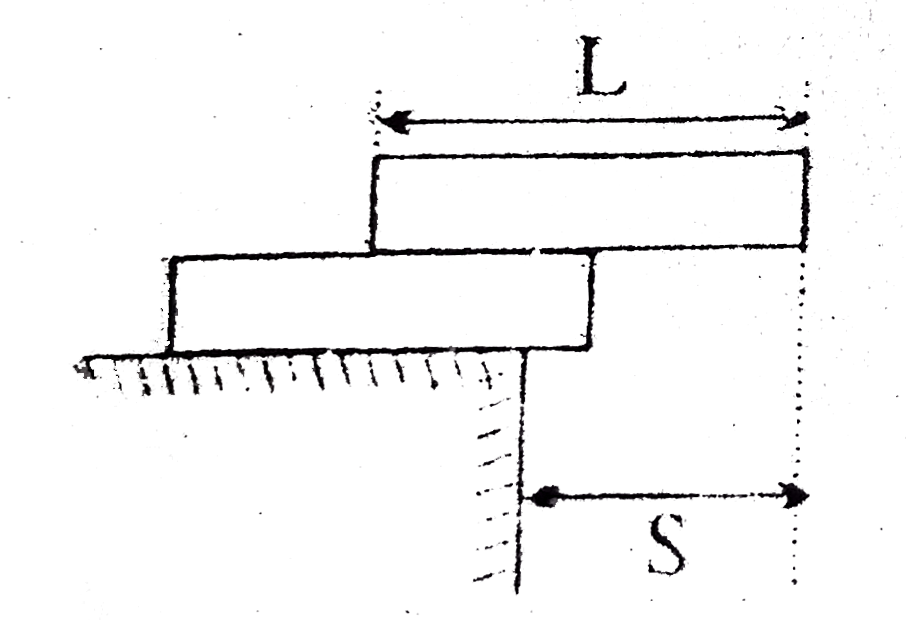
View Solution
Knowledge Check
Infinite number of bricks are placed one over the other as shown in the figure. Each succeeding brick having half the length and breadth of its preceding brick and the mass of each succeeding bricks being (1/4)th of the preceding one. Taking 'O' as the origin, the x coordinate of centre of mass of the system of bricks is at
 A−a/7B3a/7C−3a/7D−2a/7
A−a/7B3a/7C−3a/7D−2a/7Two identical bricks of length L are piled one on top of the other on a table as shown in the figure the maximum distance S the top brick can overhand the table with the system still balanced is:
 A12LB23LC34LD78L
A12LB23LC34LD78LAn infinite no of bricks are placed one over the other as shown in the figure. Each succeeding brick having half the length and breadth of its precceeding brick and the mass of each succeeding bricks 1/4th of the preceding one, take 'O' as the origin, the centre of mass of the system of bricks is at
 A−a7B−5a7C−3a7D−2a7
A−a7B−5a7C−3a7D−2a7
Given below are two quantities named I and II. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose among the possible answers.
A conical pit of base radius ‘R’ cm and height ‘H’ cm is dug and from the mud that came out after digging, a certain number of cuboidal and cylindrical bricks are made in such a way that 22 bricks of each types are made. Dimension of each cuboidal brick is 14 cm * 4 cm * 4 cm, radius and height of each cylindrical brick is 7 cm and 4 cm. Ratio of R to H is 21: 40
Quantity I: Half of height of conical pit in centimeters
Quantity II: Two less than the total number of cuboidal bricks made from the mud
View SolutionA cistern, internally measuring 150 cm x 120 cm x 110 cm. has 129600cm3 of water in it.Porous bricks are placed in the water until the cistern is full to the brim.Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in it without overflowing the water, each brick being 22.5 cm x 7.5 cm x 6.5 cm?
View SolutionA cistern, internally measuring 150 cm x 120 cm x 110 cm, has 129600 cu.cm of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm x 7.5 cm x 6.5 cm?
View SolutionA cistern, internally measuring 150 cm×120 cm×110 cm has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one seventeenth of its own volume of water. How many bricks can be put in without the water overflowing, each brick being 22.5 cm×7.5 cm×6.5 cm ?
View SolutionA cistern, internally measuring 150 cm×120 cm×110 cm has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one seventeenth of its own volume of water. How many bricks can be put in without the water overflowing, each brick being 22.5 cm×7.5 cm×6.5 cm ?
View Solution
