A glass test tube with a plane base has a diameter of 4 cm and mass 30 g. Centre of gravity of the empty test tube is at a height of 10 cm from the base. Find the amount of water to be taken in the test tube so that when it floats vertially, its centre of gravity shifts to the midpoint of the immersed portionof the tube.
The centre of gravity P of the empty tube is 10 cm above the point O. Let the height of water level taken in the tube be h cm. Midpoint of the test tube-water system be at R. Hence, part of the tube immersed in water, AC = 2×OR.

Volume of water in the tube = π(2)2h=4πhcm3
Mass of the tube + water in it = (30+4πh)g
From the condition of floatation,
π(22)×AC=30+4πh
∴ AC=2×OR=304π+h=d (say).
Taking moment about the point R,
4πh×RQ=30×PR
or, 4πh[OR−OQ]=30×[OP−OR]
or, 4πh[d2−h2]=30[10−d2]
or, 4πh[12(304π+h)−h2]=30[10−12(304π+h)]
or, h = 8.806 cm
Hence the required mass of water
= 4π×8.806=110.66g.
Topper's Solved these Questions
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - SECTION RELATED QUESTIONS
12 Videos
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
37 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - CBSE SCANNER
7 Videos
- KINETIC THEORY OF GASESBOOK - CHHAYA PUBLICATIONCHAPTER - KINETIC THEORY OF GASESEXERCISE - CBSE Scanner
9 Videos
Similar Questions
A flat bottomed thin-walled glass tube has a diameter of 4 cm and it weights 30 g. the centre of gravity of the empty tube is 10 cm above the bottom, find the amount of water which must be poured into the tube so that when it is floating vertically in a tank of water, the centre of gravity of the tube and its contents is at the midpoint ot the immersed length of the tube.
View SolutionA test tube has diameter 20 mm and height is 15 cm. The lower portion is a hemisphere. Find the capacity of the test tube. (π=3.14)

View Solution
Knowledge Check
Arrange the following steps in proper sequence to determine the relative density of liquid by using a constant immersion hydrometer.
(a) The test tube is made to float in the given liquid.
(b) The weight of the test tube with lead shots in air is determined (W1).
( c) The depth of the test tube immersed in water (h) is determined.
(d) The test tube is made to float in water.
(e ) Lead shots are added or removed from the test tube such that the test tube is immersed to the same depth (h) in the given liquid.
(f) The relative density of the liquid is measured as W1W1.
(g) The test tube is taken out from the given liquid and its weight (W2) is measured.Ab d c a e g fBb d c a e f gCb g f e a c dDb a d c e f gDuring gas of negligible mass is sealed in a test tube of mass 50gm with the helo of a stopper of mass 3.5gm. The test tube is suspended from a fixed point with help of massless string such that the test tube is horizontal and distance between point of suspension and centre of mass of test tube is 25cm. The test tube is heated to a temperature due to which stopper is ejected out horizontally while test tube completes a vertical circle of radius 25cm. The minimum velocity with which stopper should be ejected out is
A72 kmphB90 kmphC180 kmphD360 kmph
A test tube has diameter 20 mm and height is 15 cm. The lower part is a hemisphere. Find the capacity of the test tube. (π=3.14)
View SolutionAn empty glass test tube floats vertically in water to a depth of 5 cm. Now, on introducing a 8 cm liquid column into the tube, its depth in water is further increased by 4 cm. Now if the empty test tube is allowed to float vertically in the liquid, 5 cm of the tube is seen in air. Find the total length of the tube.
View SolutionA small object is 2 cm below the concave meniscus of water in a test tube . The radius of the meniscus is 5mm and μ for water is 4/3. Find the nature and position of the image.
View SolutionA vessel of cross-section 20×10−4 square metres has a capillary tube of length 10 cm and internal radius 0.5 mm at the bottom. It is initially filled with water to a height of 20 cm above the capillary tube. Find the time taken by the vessel to expt one-half of its contents, given that the viscosity of water of 0.001 SI units. Density of water = 1000 kg per cubic metre.
[Hint : See example 5]
View SolutionA test tube floats to a depth 4 cm in water and to a depth 8 cm in a liquid. The relative density of the liquid is _____.
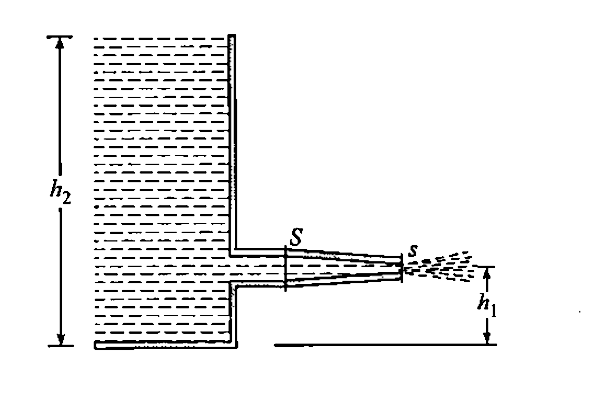
View SolutionA side wall of a wide open tank is provided with a narrowing tube through which water flows out. The cross-sectional area of the tube decreases from S=3.0cm2 to s=1.0cm2. The water level in the tank is h=4.6m heigher than in the tube. Neglecting the viscosity of water, find the horizontal component of the force tending to pull the tube out of the tank.
View Solution
