Question

Give the charge of an electron.

Explanation

Millikan.s oil drop experiment is used to determine the charge of an electron.
Principle : By adjusting electric field suitably, the motion of oil drop inside the chamber can be controlled - that is, it can be made to move up or down or even kept balanced in the field of view for sufficiently long time.
Construction :
(i) The apparatus consists of two horizontal circular metal plates A and B each with diameter around 20 cm and are separated by a small distance 1.5 cm.
(ii) These two parallel plates are enclosed in a chamber with glass walls. plates A and B are given a high potential difference around 10 kV such that electric field acts vertically downward.
(iii) A small hole is made at the centre of the upper plate A and atomizer is kept exactly above the hole to spray the liquid.
(iv) When a fine droplet of highly viscous liquid (like glycerine) is sprayed using atomizer, it falls freely downward through the hole of the top plate under the influence of gravity.
Working :
(i) Few oil drops in the chamber can acquire electric charge (negative charge) because of friction with air or passage of x-rays in between the parallel plates.
(ii) The chamber is illuminated by light which is passed horizontally and oil drops can be seen clearly using microscope placed perpendicular to the light beam. These drops can move either upwards or downward.
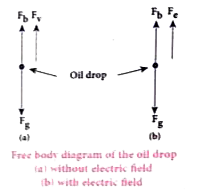
(iii) Let m be the mass of the oil drop and q be its charge. Then the forces acting on the droplet are
(a) gravitational force `F_(g)=mg`
(b) electric force `F_(e)=qE`
( c) buoyant force `F_(b)`
(d) viscous force `F_(v)`

(iv) When the electric field is switched off, the oil drop accelerates downwards. Due to the presence of air drag forces, the oil drops easily attain its terminal velocity and moves with constant velocity.
(v) This velocity can be carefully measured by noting down the time taken by the oil drop to fall through a predetermined distance. The free body diagram of the oil drop is shown if Figure (a), we note that viscous force and buoyant force balance the gravitational force.
(vi) Let the gravitational force acting on the oil drop (downward) be `F_(g)` = mg assume that oil drop to be spherical in shape. Let `rho` be the density of the oil drop, and r be the radius of the oil drop, then the mass of the oil drop can be expressed in terms of its density as
(vii) `rho=m/V` `rArrm=rho(4/3pir^(3))" "(therefore"volume of the sphere",V=4/3pir^(3))`
The gravitational force can be written in terms of density as
`F_(g)=mgrArrF_(g)=rho(4/3pir^(3))g`
Let `sigma` be the density of the air, the upthrust force experienced by the oil drop due to displaced air is
`F_(b)=sigma(4/3pir^(3))g`
(viii) Once the oil drop attains a terminal velocity v, the net downward force acting on the oil drop is equal to the viscous force acting opposite to the direction of motion of the oil drop. From Stokes law, the viscous force on the oil drop is
`F_(v)=6pirveta`
(ix) From the free body diagram as shown in Figure (a), the force balancing equation is
`F_(g)=F_(b)+F_(v)`
`rho(4/3pir^(3))g=sigma(4/3pir^(3))g=6pirveta`
`4/3pir^(3)(rho-sigma)g=6pirveta`
`2/3pir^(3)(rho-sigma)g=3pirveta`
`r=[(9etav)/(2(rho-sigma)g)]^(1/2)" "...(1)`
Thus, equation (1) gives the radius of the oil drop.
(x) When the electric field is switched on, charged oil drops experience an upward electric force (qE). Among many drops, one particular drop can be chosen in the field of view of microscope and strength of the electric field is adjusted to make that particular drop to be stationary. Under these circumstances, there will be no viscous force acting on the oil drop. Then, from the free body diagram shown Figure (b), the net force acting on the oil droplet is
`F_(e)+F_(b)=F_(g)`
`rArrqE+4/3pir^(3)sigmag=4/3pir^(3)rhog`
`rArrqE=4/3pir^(3)(rho-sigma)g`
`rArrq=4/(3E)pir^(3)(rho-sigma)g" "...(2)`
Substituting equation (1) in equation (2), we get
`q=(18E)/E((eta^(3)v^(3))/(2(rho-sigma)g))^(1/2)`