Derive an expression for the pressure of an ideal gas in a container from Kinetic Theory and hence give Kinetic Interpretation of Temperature.

Text Solution

Verified by Experts

Consider a cube of side .l. and an ideal gas is filled in it. Let the co-ordinates, X, Y and Z will coincide with the sides of the cube. Let velocities of gas molecules along these directions are $V_{x}, V_{y} and V_{z}$ . Consider a gas molecule moving along X-axis with a velocity $V_{x}$ . Its motion is perpendicular to Y-Z plane. Let the gas molecule suffered elastic collision with Y-Z plane and bounced back. In this case the velocities $V_{y} and V_{z}$ are not considered because collision is along X-direction only.

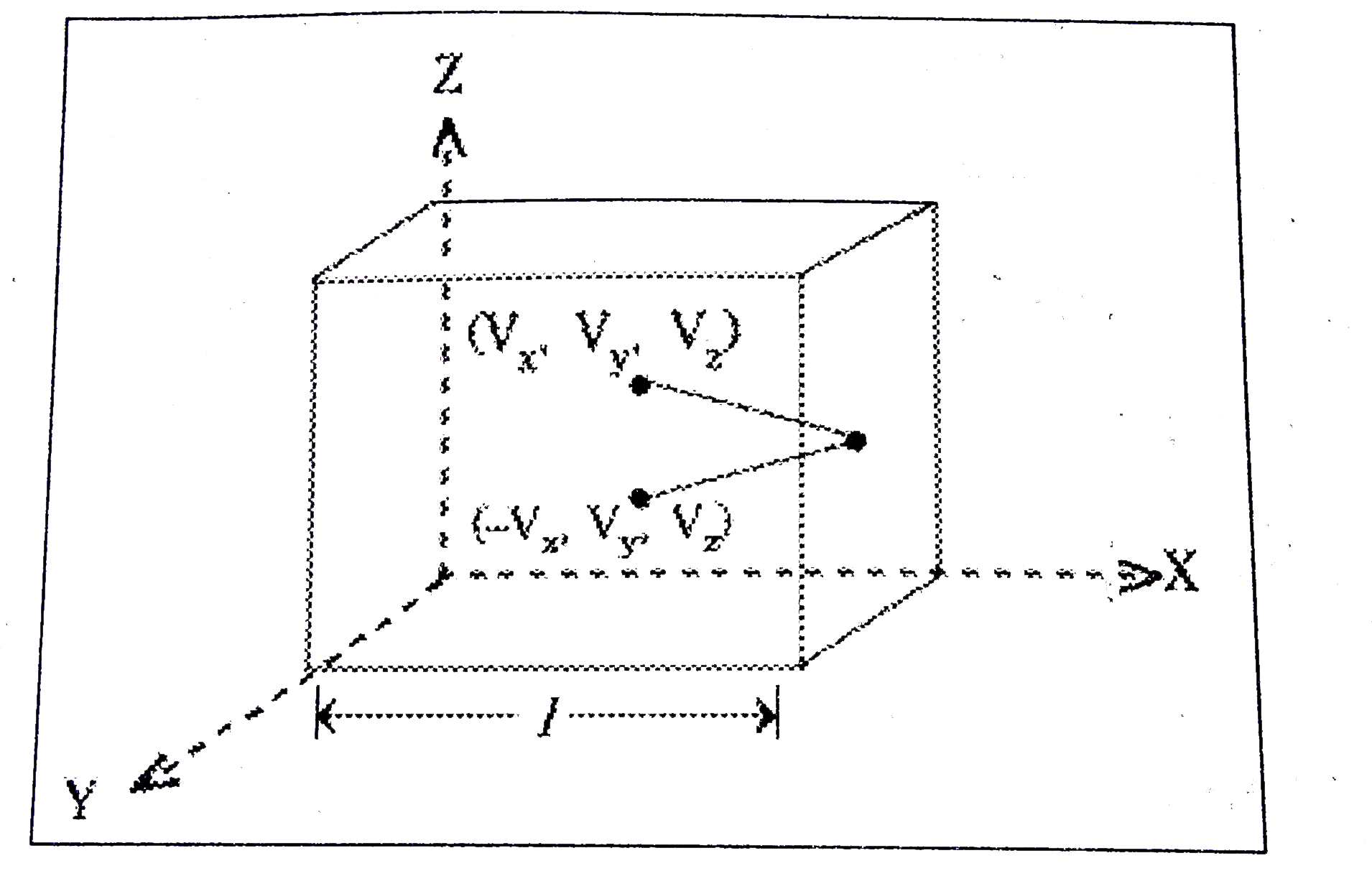
Change in momentum along X-direction is final momentum $(- m V_{x})$ - initial momentum $(m V_{x}) = - 2 m V_{x}$ ...........(1)
Let area of one side of the cube is A. Then during the time $Δ t$ only the molecules at a distance of $V_{x} Δ t$ will collide with the walls. Let number of gas molecules in the volume $A V Δ t$ are say.n.. In these molecules half of the molecules will move towards the wall and remaining will move away from the wall.
$∴$ Amount of momentum transferred to the wall = Q
$= 2 m V_{x} \times$ number of molecules collided with wall
$∴ Q = 2 m V_{x} (\frac{1}{2} n A V_{x} Δ t)$
Pressure on Y - Z plane =
$P_{x} = \frac{Rate of change in momentum}{Area}$
$∴ P = \frac{Force}{Area} = \frac{Q / Δ t}{A}$
$= \frac{2 m V_{x} \frac{.1}{2} n A V_{x} Δ t}{A Δ t} = n m V_{x}^{2}$
If behaviour of gas is isotropic that is equal in all directions then $V_{x} = V_{y} = V_{z}$
$∴$ Root mean square velocity of gas
$= \frac{V_{x}^{2} + V_{y}^{2} + V_{z}^{2}}{3} = \frac{1}{3} {¯ ¯ ¯ V}^{2}$
Where ${¯ ¯ ¯ V}^{2} = V_{x}^{2} + V_{y}^{2} + V_{z}^{2}$
$∴$ Pressure of gas $P = \frac{1}{3} n m {¯ ¯ ¯ V}^{2}$
From Pascal.s law pressure is same throught the container so pressure in any direaction (say x,y or z) is same.
Kinetic interpretation of temperature :
From gas equation
$P V = \frac{1}{3} n m {¯ ¯ ¯ V}^{2} . V = \frac{2}{3} N (\frac{1}{2}) m {¯ ¯ ¯ V}^{2})$
Where $N = n V$ and $\frac{1}{2} m {¯ ¯ ¯ V}^{2}$ = kinetic energy
for ideal gas internal energy is purely kinetic energy.
$∴ E = n \frac{1}{2} m {¯ ¯ ¯ V}^{2} ∴ P V = \frac{3}{2} E$
But $P = K_{B} N T$
$∴ E = \frac{3}{2} P V = \frac{3}{2} K_{B} N . T$
But $\frac{E}{N} = \frac{1}{2} m V^{2} and \frac{E}{N} = \frac{3}{2} K_{B} T$
$∴ \frac{E}{N} α T$ is the average kinetic energy of gas molecule is proportional to absolute temperature of gas. But it does not depend on volume of container.

Updated on:21/07/2023

Kinetic theory of an ideal gas gives the relation
A $\frac{1}{3} n m V^{2}$
B $\frac{1}{2} n m {¯ v}^{2}$
C $P V = μ R T$
DNone of these
An ideal gas obeying the kinetic theory of gases can be liquefied if
AIts temperature is more than its critical temperature $(T_{c})$
BIts pressure is more than its critical pressure $(P_{c})$
CIts pressure is more than $P_{c}$ at a temperature less than $T_{c}$
DIt cannot be liquefied at any value of $P$ and $T$
An ideal gas obeying the kinetic theory of gases can be liquefied if
AIts temperature is more than its critical temperature $(T_{c})$
BIts pressure is more than its critical pressure $(P_{c})$
CIts pressure is more than $P_{c}$ at a temperature less than $T_{c}$
DIt cannot be liquefied at any value of $P$ and $T$