In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.

Text Solution

Verified by Experts

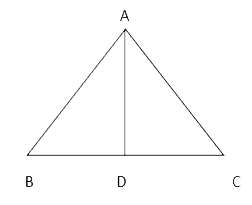
$A D ⊥ B C ∴ I n Δ A B D, A B^{2} = A D^{2} + B D^{2}$
$\Rightarrow A B^{2} = A D^{2} + \frac{B C^{2}}{4} or 4 A B^{2} + B C^{2}$
$\Rightarrow 3 A B^{2} = 4 A D^{2}$

Updated on:21/07/2023

|

Class 10 MATHS SAMPLE PAPER 2019

Similar Questions

In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
View Solution
Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
View Solution
Prove that three times the square of any side of an equilateral-triangle is equal to four times the square of the altitude.
View Solution
Prove that three times the square of any side of an equilateral-triangle is equal to four times the square of the altitude.
View Solution
In an equilateral triangle with side a, prove that the altitude is of length $\frac{a \sqrt{3}}{2}$
View Solution
In an equilateral triangle with side a, prove that the altitude is of length $\frac{a \sqrt{3}}{2}$
View Solution
In a right angled triangle, five times the square on the hypotenuse is equal to four times the sum of the squares on the medians drawn from the acute angles. Prove it.
View Solution
Prove that three times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares of the medians of the triangle.
View Solution
Prove that three times the sum of the squares on the sides of a triangle is equal to four times the sum of the square on the medians of the triangle.
View Solution
Prove that three times the sum of the squares of the sides of a triangle is equal to fourtimes the sum of the squares of the medians of the triangle.
View Solution

Recommended Questions

Home
Ask Doubt
Profile