Prove that ^nCn0C0−n+1Cn1C1+n+2Cn2C2≡(−1)n.
.nC0.nC0−.nC1.n+1C1+.nC2.n+2C2−.....
=.nC0.nCn−.nC1.n+1Cn+.nC2.n+2Cn−....
= Coefficient of xn in [.nC0(1+x)n−.nC1(1+x)n+1+.nC2(1+x)n+2+.....+(−1)n.nCn(1+x)2n]
= Coefficient of x2 in (1+x)n[.nC0−.nC1(1+x)+.nC2(1+x)2−......+(−1)n.nCn(1+x)n]
= Coefficient of xn in (1+x)n[1−(1+x)]n
= Coefficient of xn in (1+x)n(−x)n
=(−1)n
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Exercise 8.810videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Exercise (Single)90videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Exercise 8.610videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank20videos
AREA UNDER CURVES
- BOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank31videos
BINOMIAL THEORM
Similar Questions
Prove that ^nCn0C0−n+1Cn1C1+n+2Cn2C2≡(−1)n.
View SolutionProve that nC2n0Cn−nC2n−11Cn+nC2×2n−2Cn++(−1)n^nCnnCn=1.
View SolutionProve that ^nC2n0Cn−nC2n−21Cn+nC2n−42Cn=2n.
View SolutionIf (1+x)n=C0+C1x+C2x2+…+Cnxn, prove that C0Cn−C1Cn−1+C2Cn−2−…+(−1)nCnC0=0 or (−1)n/2n!(n/2)!(n/2)! , according as n is odd or even .
View SolutionProve that .nC0−.nC1+.nC2−.nC3+……+(−1)r+.nCr+……=(−1)r×.n−1Cr.
View SolutionProve that (^(2n)C0)2+(^(2n)C1)2+(^(2n)C2)2−+(^(2n)C2n)2−(−1)n^(2n)Cn.
View SolutionProve that (.2nC0)2−(.2nC1)2+(.2nC2)2−….+(.2nC2n)2=(−1)n.2nCn
View SolutionProve that: ^(2n)C0−3.2nC1+32.2nC2−..+(−1)2n..32n^(2n)C2n=4n for all value of N
View SolutionProve that :nC0.2nCn−nC1.2n−2Cnn+nC2.2n−4Cnn+......=2n
View SolutionIn C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
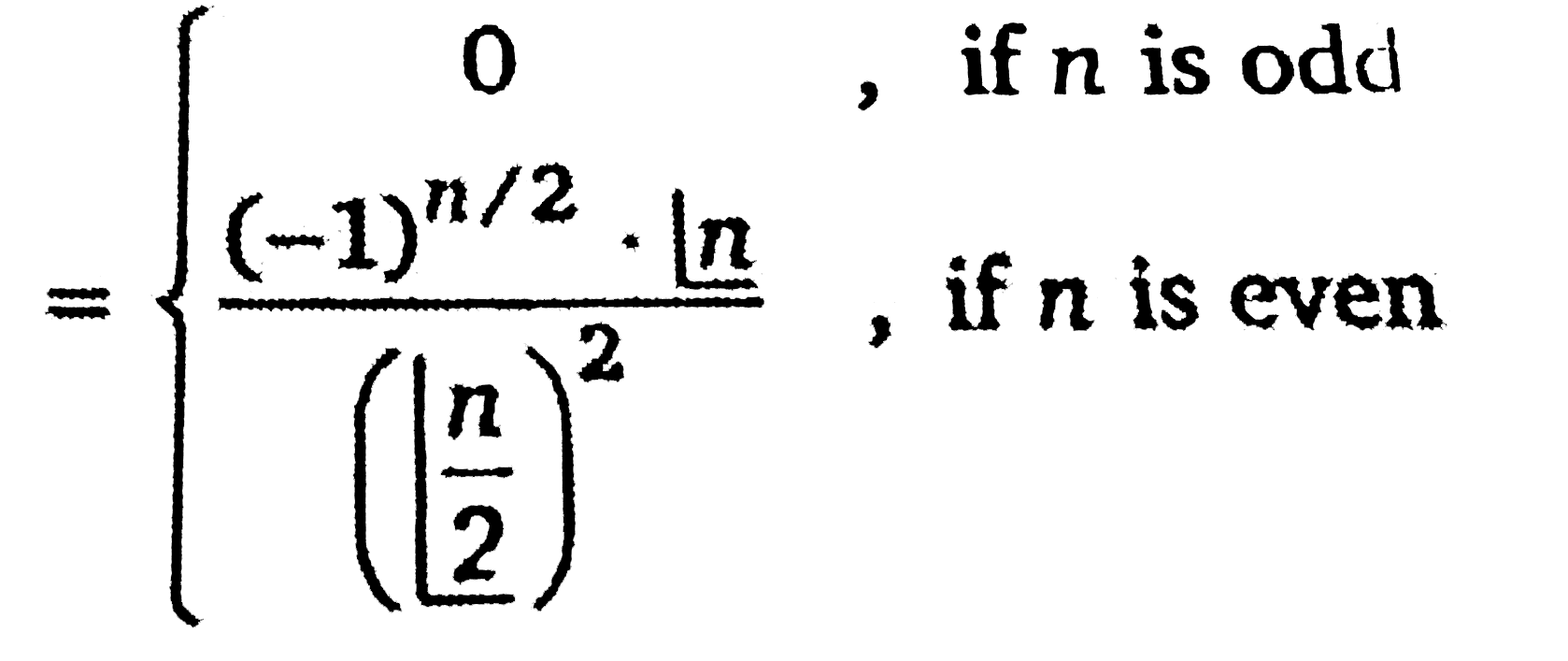
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
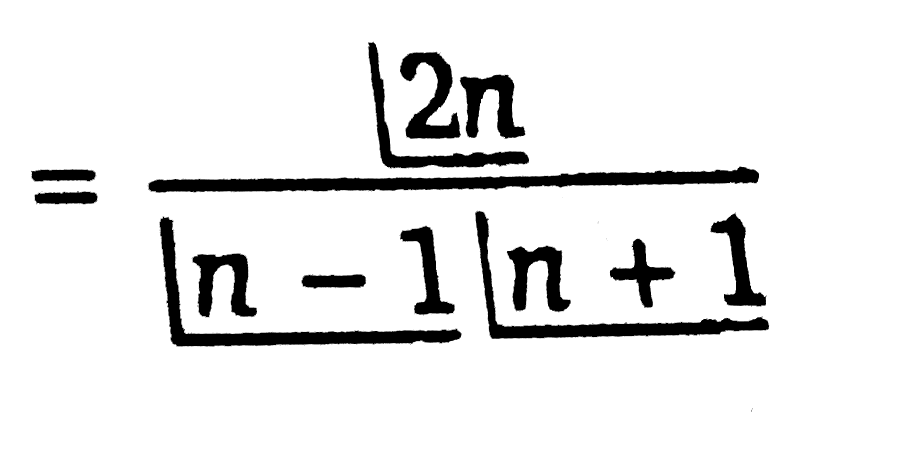 View Solution
View Solution

