Write the formula to find the sum of first n terms of an Arithmetic progression, whose first term is a and the last term is an.Solution in Kannada
Step by step video & image solution for Write the formula to find the sum of first n terms of an Arithmetic progression, whose first term is a and the last term is a_n. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Unless stated otherwise, use π=227.
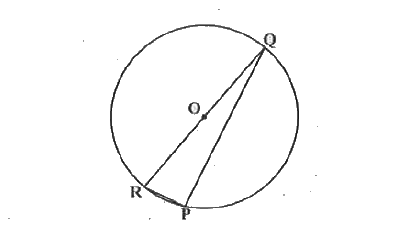
Find the area of the shaded region in Fig. 5.19, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
View SolutionThe first term of an arithmetic progression is 1 and the sum of the first nine terms equal to 369. The first and the ninth term of a geometic progression colncide with the first and the ninth term of the arithmetic progression. Find the seventh term of the geometric progression.
View SolutionWrite the formula to find the sum of first n terms of an Arithmetic progression, whose first term is a and the last term is an.
View SolutionThe sum of first 'n' terms of an arithmetic progression is 210 and sum of its first (n-1) terms is 171. If the first term 3, then write the arithmetic progression.
View SolutionWhat is the sum of the first 17 terms of an arithmetic progression if the first term is -20 and last term is 28?
View SolutionWhat is the sum of the first 9 terms of an arithmetic progression if the first term is 7 and the last term is 55?
View SolutionWhat to the sum of the first 13 terms of an arithmetic progression if the first term to -10 and last term is 26?
View SolutionIn an arithmetic progression of 50 terms, the sum of first ten terms is 210 and the sum of last fifteen terms is 2565. Find the arithmetic progression.
View SolutionIn an arithmetic progression of 50 terms, the sum of first ten terms is 210 and the sum of last fifteen terms is 2565. Find the arithmetic progression.
View SolutionThe first term of an arithmetic progression is 1 and the sum of the first nine terms equal to 369. The first and the ninth term of a geometric progression coincide with the first and the ninth term of the arithmetic progression. Find the seventh term of the geometric progression.
View SolutionThe first term of an arithmetic progression is 1 and the sum of the first nine terms equal to 369. The first and the ninth term of a geometric progression coincide with the first and the ninth term of the arithmetic progression. Find the seventh term of the geometric progression.
View SolutionThe sum of the first fifteen terms of an arithmetical progression is 105 and the sum of the next fifteen terms is 780. Find the first three terms of the arithmetical progression,.
View SolutionThe first term of an arithmetic progression is 1 and the sum of the first nine terms equal to 369. The first and the ninth term of a geometric progression coincide with the first and the ninth term of the arithmetic progression. Find the seventh term of the geometric progression.
View SolutionTwo arithmetic progressions have the same numbers. The reatio of the last term of the first progression to the first term of the second progression is equal to the ratio of the last term of the second progression to the first term of first progression is equal to 4. The ratio of the sum of the n terms of the first progression to the sum of the n terms of teh first progression to the sum of the n terms of the second progerssion is equal to 2.
The ratio of their first term is
View SolutionThe first term of an arithmetic progression is 1 and the sum of the first nine terms equal to 369. The first and the ninth term of a geometric progression coincide with the first and the ninth term of the arithmetic progression. Find the seventh term of the geometric progression.
View Solution
