In the following figure, find the locus of centroid of triangle PAB, where AP perpendicular to PB.

∴ Slope of AP =2t
⇒ Slope of BP =−t2
So, equation of line BP is y−2t=−t2(x−t2).
Putting y = 0, we get point B as (t2+4,0). Now , let centroid of ΔPAB be (h,k).
∴ h=t2+t2+43andk=2t3
Eliminating 't', we get
3h−4=2(3k2)2
∴ 3x−4=9y22, which is the required locus.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise 5.111videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise 5.217videos
PARABOLA
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank19videos
PERMUTATION AND COMBINATION
Similar Questions
Knowledge Check
- Question 1 - Select One
Let AB be a chord of the circle x2+y2=r2 subtending a right angle at the centre. Then the locus of the centroid of the triangle PAB as P moves on the circle is
Aa parabolaBa circleCan ellipseDa pair of straight lines
A variable line through the point P(2,1) meets the axes at AandB . Find the locus of the centroid of triangle OAB (where O is the origin).
View SolutionA variable line through the point P(2,1) meets the axes at A an d B . Find the locus of the centroid of triangle OAB (where O is the origin).
View SolutionLet AB be chord of contact of the point (5,−5) w.r.t the circle x2+y2=5 . Then find the locus of the orthocentre of the triangle PAB , where P is any point moving on the circle.
View SolutionThe locus of P such that area of triangle PAB is 12 sq units
View SolutionA straight line moves in such a way that the length of the perpendicular upon it from the origin is always p. Find the locus of the centroid of the triangle which is formed by the line and the axes.
View SolutionA straight line moves in such a way that the length of the perpendicular upon it from the origin is always p. Find the locus of the centroid of the triangle which is formed by the line and the axes.
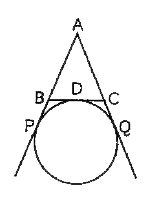
View SolutionIn the figure, find the perimeter of ΔABC, if AP =12 cm.
 View Solution
View Solution