Consider a pyramid OPQRS located in the first octant (x≥0,y≥0,z≥0) with O as origin, and OP and OR along the x-axis and the y-axis,respectively. The base OPQR of the pyramid is asqu are with OP=3. The point S is directly above the mid-point T of diagonal OQ such that TS=3.Then
1.the acute angle between OQ and OS is π/3
2.the equataion of the plane containing th etriangle OQS is x-y=0
3.the length of the perpendicular from P to the plane containing the triagle OQS is 3√2
4.the perpendcular distance from O to the straight line containing RS is √152
b.,c.,d
Direction rations ofOQ≡(3,3,0)
Direction rations of OS≡(32,32,3)
if θ is the angle between OS and OR , then
cosθ=3×32+3×32√32+32√(32)2+(32)2+32=1√3

∴ hence (a) is wrong
Normal t plane OQS,
−−→OQ×−−→OS=±∣∣
∣
∣∣ˆiˆjˆk33032323∣∣
∣
∣∣=±(9ˆi−9ˆj)
∴Equation of plane OQS is
(xˆi+yˆj+zˆk).(9ˆi−9ˆj)=0
⇒x−y=0
Distance of p from plane OQS = distancae PT = distance OT =3√2
Equation of RS is x−032−0=y−332−3=z−03−0
orx32=y−3−32=z3
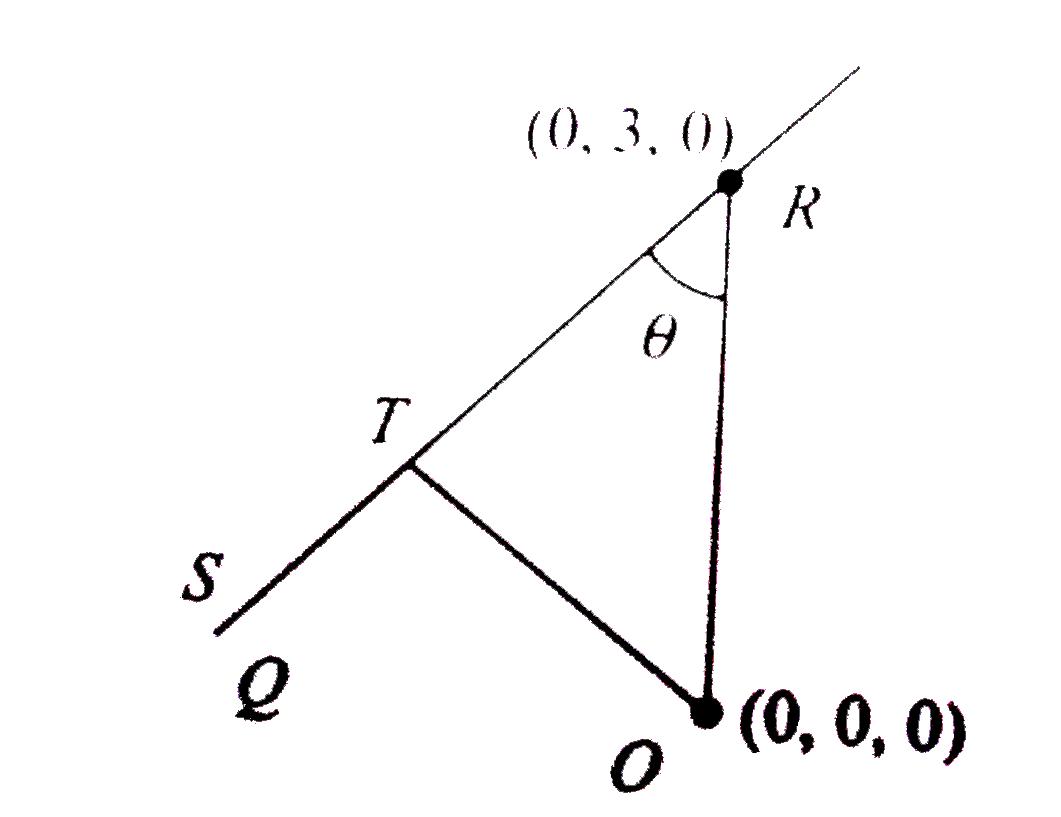
ANgle between line Rs and OR
cosθ=0+3(−32)+03√(32)2+(32)2+32=−1√6
distance =OT=ORsinθ=3√1−16=3√56=√152
Similar Questions
Consider a pyramid OPQRS located in the first octant (x≥0,y≥0,z≥0) with O as origin and OP and OR along the X-axis and the Y-axis , respectively. The base OPQRS of the pyramid is a square with OP=3. The point S is directly above the mid point T of diagonal OQ such that TS=3. Then,
View SolutionConsider the cube in the first octant with sides OP,OQ and OR of length 1, along the x-axis, y-axis and z-axis, respectively, where O(0,0,0) is the origin. Let S(12,12,12) be the centre of the cube and T be the vertex of the cube opposite to the origin O such that S lies on the diagonal OT. If →p=−→SP,→q=−−→SQ,→r=−−→SR and →t=−→ST then the value of ∣∣(→p×→q)×(→r×(→t)∣is
View Solution
Knowledge Check
Consider a pyramid OPQRS located in the first octant (x≥0,y≥0,z≥0) with O as origin and OP and OR along the X-axis and the Y-axis , respectively. The base OPQRS of the pyramid is a square with OP=3. The point S is directly above the mid point T of diagonal OQ such that TS=3. Then,
A1.the acute angle between OQ and OS is π/3B2.the equataion of the plane containing th etriangle OQS is x-y=0C3.the length of the perpendicular from P to the plane containing the triagle OQS is 3√2D4.the perpendcular distance from O to the straight line containing RS is √152Consider a pyamid OPQRS locaated in the first octant (x≥0,y≤0,z≤0) with O as origin , and OP an OR along the x-axis and y-axis respectively. The base OPQR of the pyramid is a square with OP=3 . The point S is directly above the mid-point T of the diagonal OQ such that TS=3 , Then , the angle between OQ and OS, is
Aπ3Bπ6Ccos−11√3Dcos−113If a line OP through the origin O makes angles α,45∘and60∘ with x, y and z axis respectively then the direction cosines of OP are.
A1√2,12,12B12,12,1√2C12,1√2,12Dnone of these
Consider the cube in the first octant with sides OP,OQ and OR of length 1, along the x-axis, y-axis and z-axis, respectively, where O(0,0,0) is the origin. Let S(12,12,12) be the centre of the cube and T be the vertex of the cube opposite to the origin O such that S lies on the diagonal OT. If →p=−→SP,→q=−−→SQ,→r=−−→SR and →t=−→ST then the value of ∣∣(→p×→q)×(→r×(→t))∣∣is
View SolutionA cube in the first octant has sides OP, OQ and OR of length 1, along the z-axis, y-axis and z-axis, respectively, where O(0, 0, 0) is the origin. Let the centre of the cube be at S(12.12,12) and T be the vertex of the cube opposite to the origin O such that S lies on the diagonal OT. If →p=−→SP,→q=−−→SQ,→r=−−→SR and →t=−→ST, then the value of ∣∣(→p×→q)×(→r×→t)∣∣ is:
View SolutionIF O be the origin and OP makes angles 450and600 with the positive directionof x and y-axes respectively and OP=12 units find the coordinates of P.
View SolutionConsider the point P as the origin and time OP as the x-axis in the situation shown in the figure. Which of the following represents the coordinates of the image of the point object O. (Take OP=20cm)
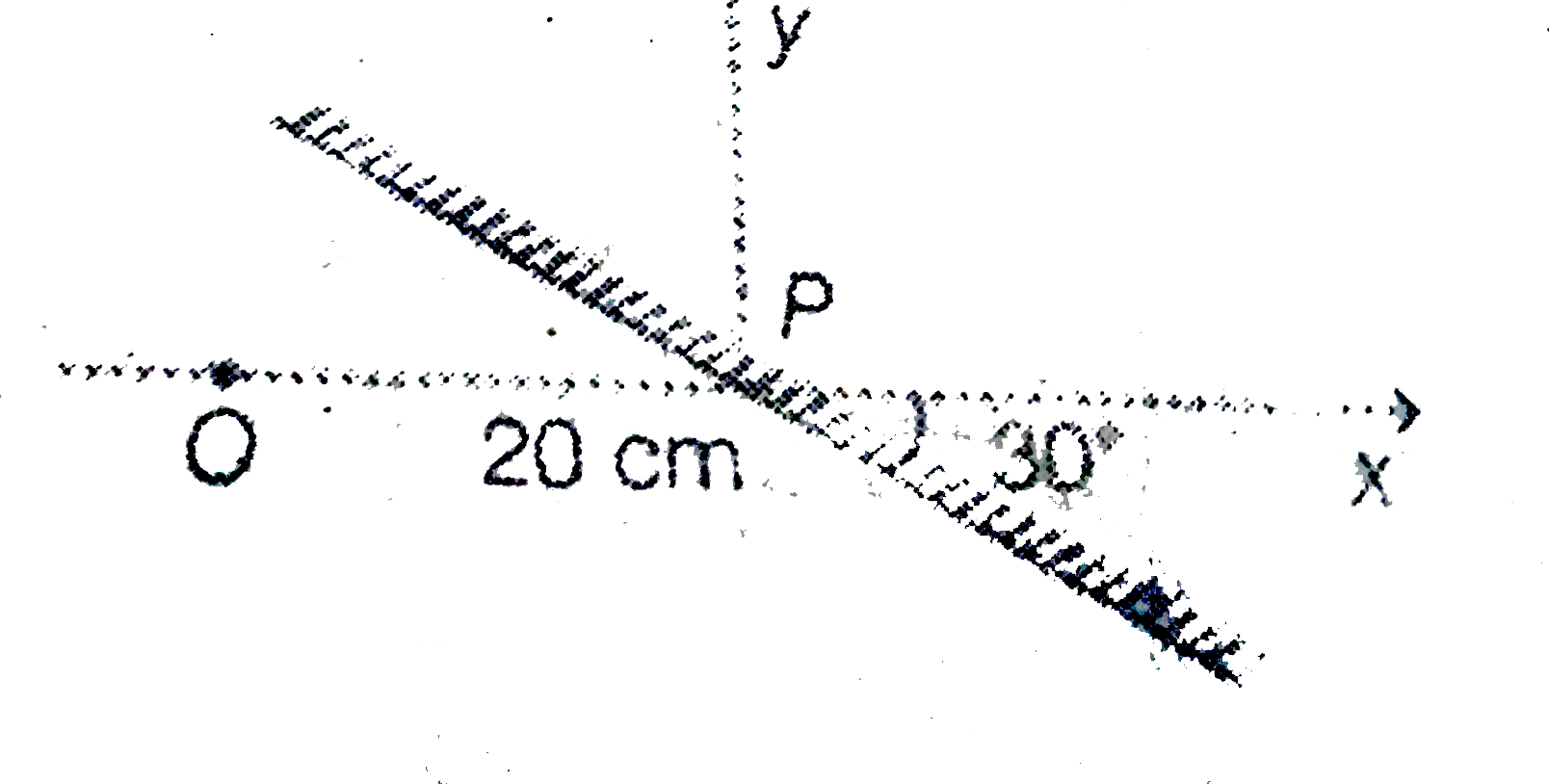
View SolutionConsider the point P as the origin and time OP as the x-axis in the situation shown in the figure. Which of the following represents the coordinates of the image of the point object O. (Take OP=20cm)
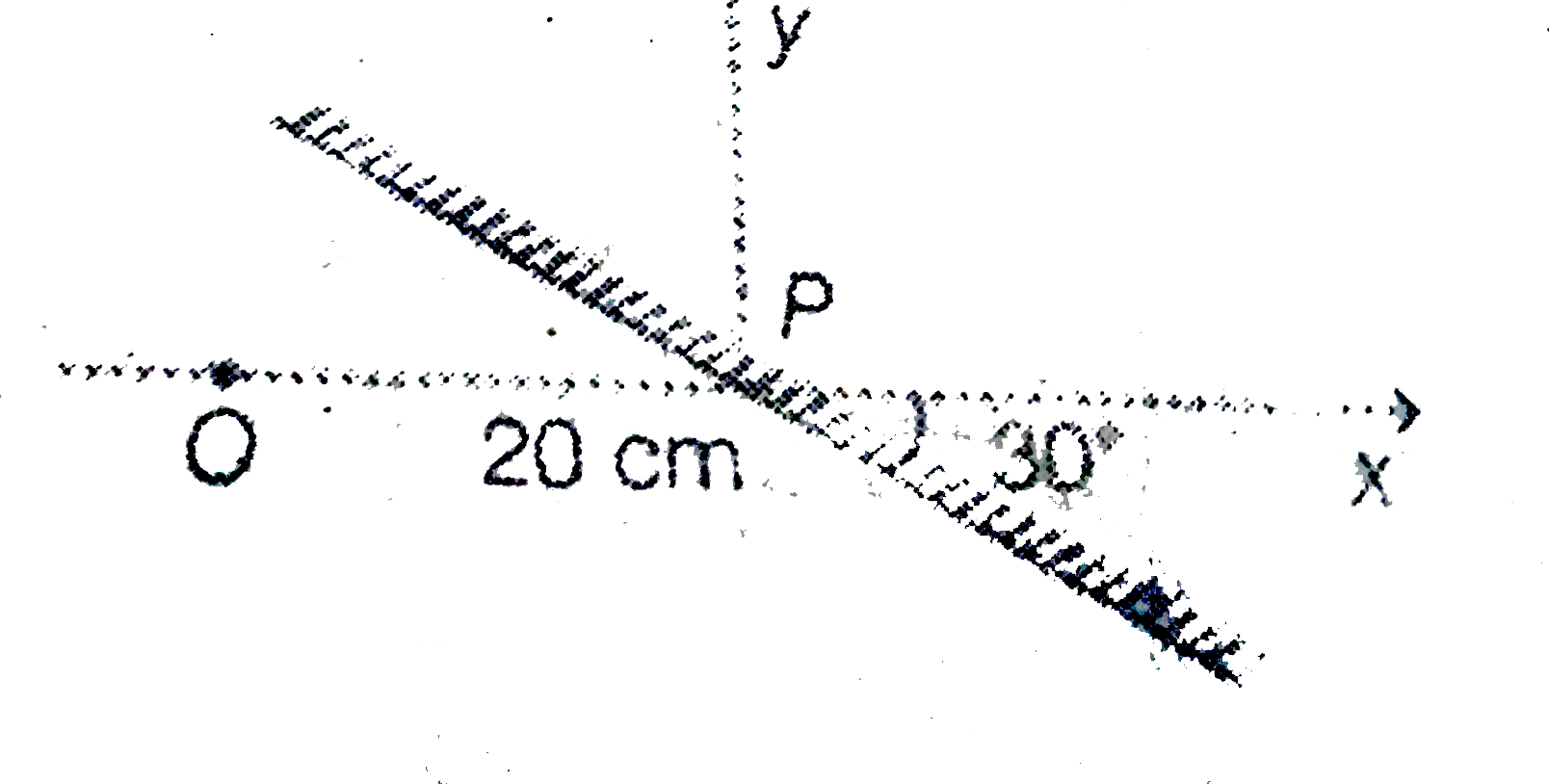
View Solution
