A parabola mirror is kept along y2=4x and two light rays parallel to its axis are reflected along one straight line. If one of the incident light rays is at 3 units distance from the axis, then find the distance of the other incident ray from the axis.
Step by step video & image solution for A parabola mirror is kept along y^2=4x and two light rays parallel to its axis are reflected along one straight line. If one of the incident light rays is at 3 units distance from the axis, then find the distance of the other incident ray from the axis. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Suppose a circle C of radius √2 touches the Y-axis at the origin (0,0). A ray of light L, parallel to the X-axis, reflects on a point P on the circumference of C, and after reflection, the reflected ray L' becomes parallel to the Y-axis. Find the distance between the ray L and the X-axis.
View SolutionFind the distance CQ if incident light ray parallel to principal axis is incident at an angle i. Also, find the distance CQ if i→0 .

View Solution
Knowledge Check
A ray of light is incident on a concave mirror. If it is parallel to the principal axis, the reflected ray will
Apass through the focusBpass through the centre of curvatureCpass through the poleDretrace its pathA ray of light is incident on a concave mirror . It is parallel to the principal axis and its height from principal axis is equal to the focal length of the mirror. The ratio of the distance of point B to the distance of the focus from the centre of curvature is (AB is the reflected ray)
_E01_055_Q01.png) A2√3B√32C23D12
A2√3B√32C23D12A ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.ADACBBCDABCBACDDDBAC
A ray of light parallel to principal axis after reflection from concave mirror passes through……….. .
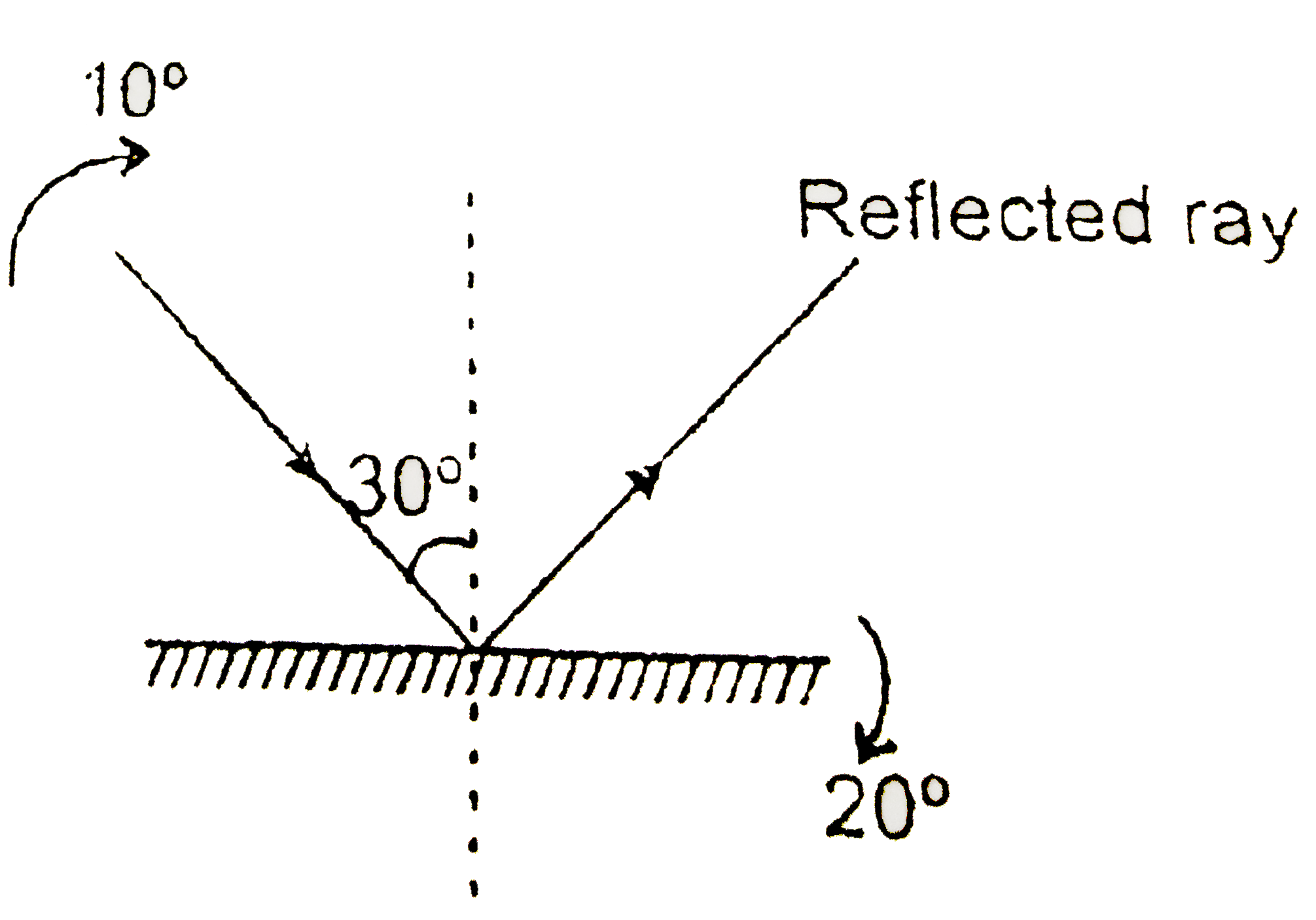
View SolutionFigures shows a plane mirror on which a light ray is incident, if the incident light ray is turned by 10∘ and the mirror by 20∘ as shown , find the angle turned by the reflected ray.
View SolutionA ray of light along x+√3y=√3 gets reflected upon reaching x-axis, the equation of the reflected ray is
View SolutionA ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.
View SolutionA ray of light along x+√3y=√3 gets reflected upon reaching x-axis.The equation of the reflected ray is
View Solution
