The correct Answer is:a→p;q
Projection of →α+βˆj on√3ˆi+ˆj is√3
∣∣
∣∣αˆi+βˆj.(√3ˆi+ˆj2)∣∣
∣∣=√3
⇒√3α+β=±2√3
⇒√3α+(α−2√3)=±2√3
⇒3α+α−2=±6
4α=8,m−4
⇒α2,−1
Note : solutions of the remaining parts are given in their respective chapters.
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Single Question)
28 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - JEE Previous Year (Multiple Question)
11 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.3
18 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
1316 Videos
- LIMITS AND DERIVATIVESBOOK - CENGAGECHAPTER - LIMITS AND DERIVATIVESEXERCISE - Solved Examples And Exercises
320 Videos
Similar Questions
The scalar →A.(→B+→C)×(→A+→B+→C) equals (A) 0 (B) [→A→B→C]+[→B→C→A] (C) [→A→B→C] (D) none of these
View SolutionLet →a=a1ˆi+a2ˆj+a3ˆk,→a=b1ˆi+b2ˆj+b3ˆk and →a=c1ˆi+c2ˆj+c3ˆk be three non- zero vectors such that →c is a unit vectors perpendicular to both the vectors →c and →b. If the angle between →a and →n is π6 then
∣∣ ∣∣a1a2a3b1b2b3c1c2c3∣∣ ∣∣ is equal to
View SolutionIf →a,→b,→cand→d are four non-coplanar unit vectors such that →d makes equal angles with all the three vectors →a,→b,→c then prove that [→d→a→b]=[→d→c→b]=[→d→c→a]
View SolutionLet A(0,1),B(1,1),C(1,−1),D(−1,0) be four points. If P is any other point, then PA+PB+PCPD≥d, when [d] is where [.] represents greatest integer.
View SolutionEvaluate the limit: (lim)x→0sinaxsinbx
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
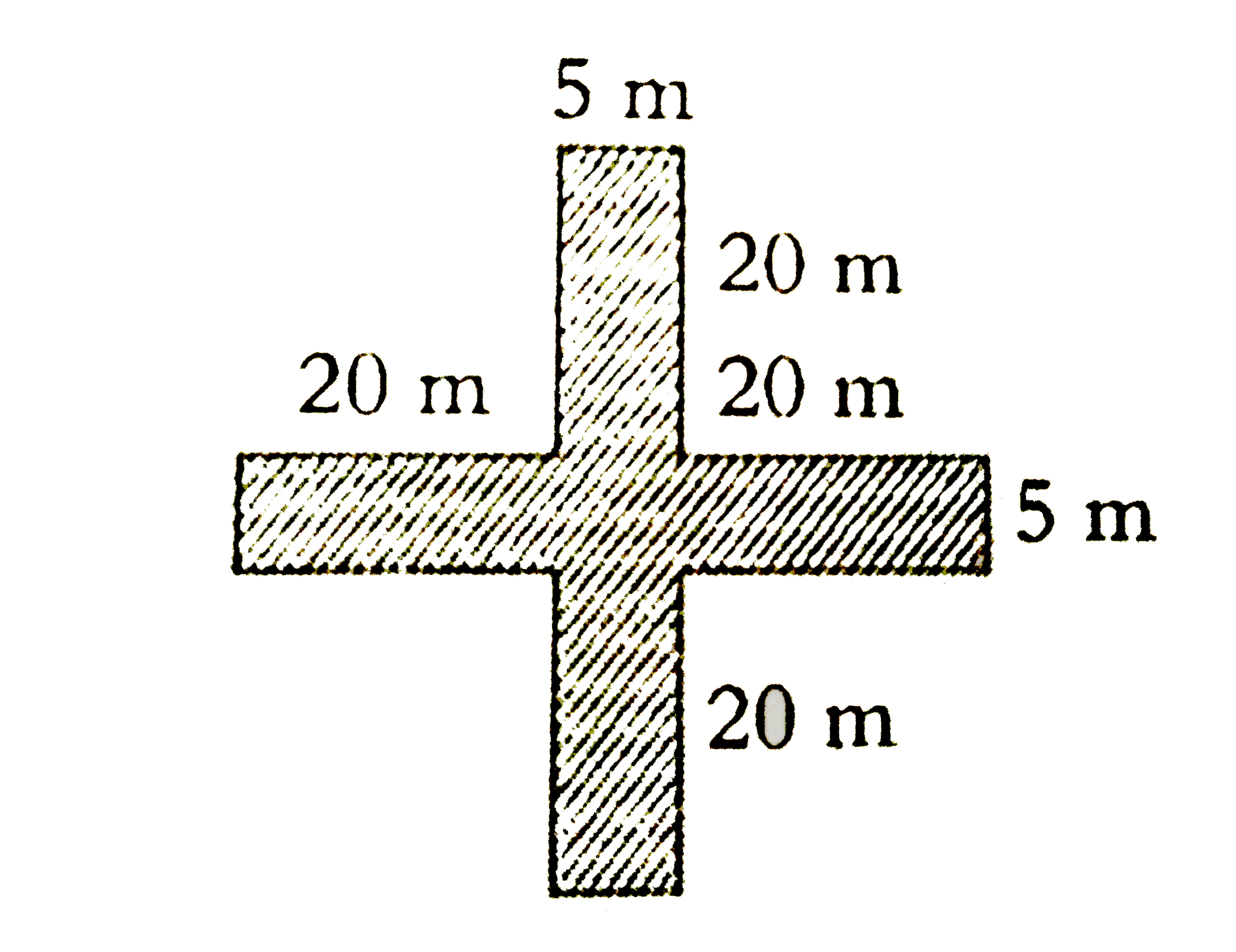
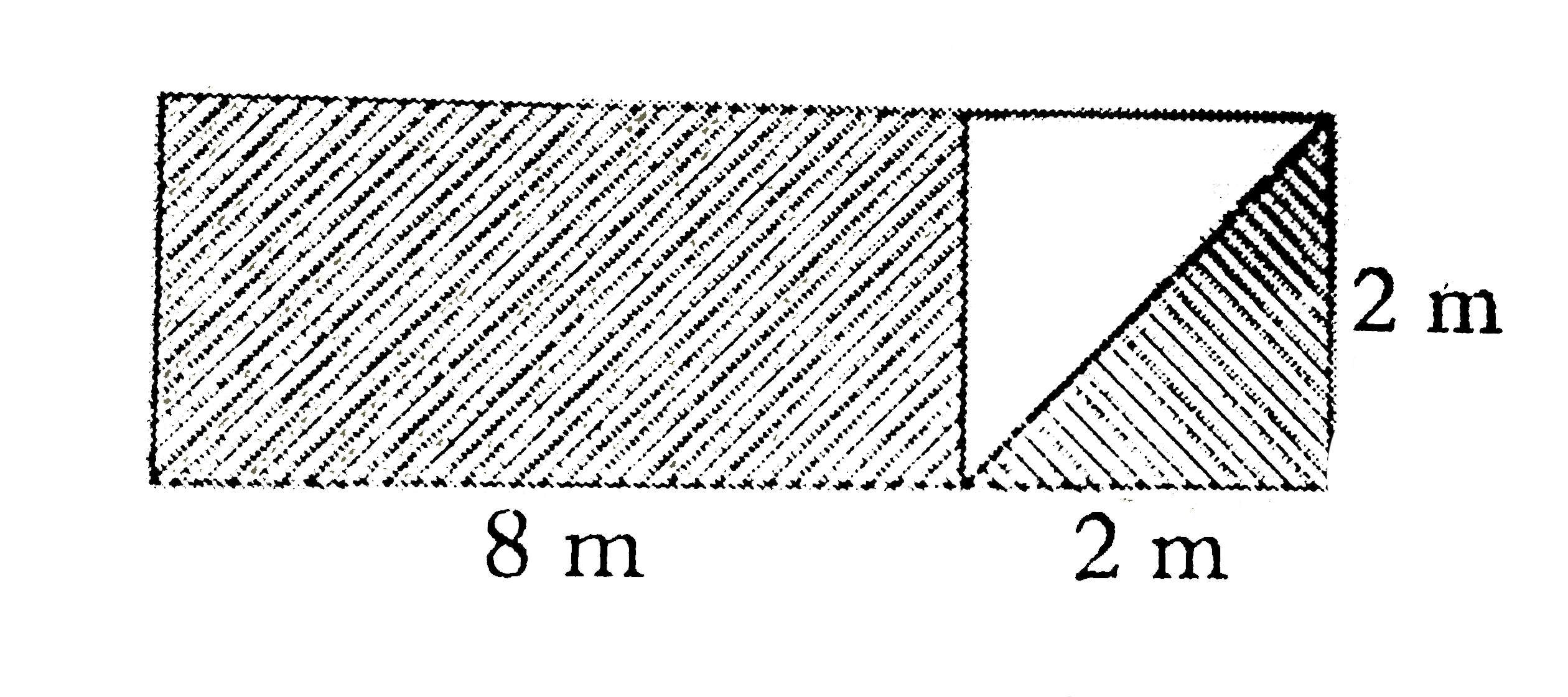
View SolutionThe area of the shaded part in the figure given below is ______.
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution

