y=0.25sin(10πx−2πt) समीकरण जिसमें x और y मीटर में हैं और t सेकण्ड में है, उस तरंग को व्यक्त करता है जिसका गतिपथ है
ऋणात्मक x दिशा में और आवृत्ति 1 हर्ट्ज है।
धनात्मक x दिशा में, आवृत्ति π हर्ट्ज और तरंगदैर्ध्य λ=0.2 मी है।
धनात्मक x दिशा में, आवृत्ति 1 हर्ट्स और तरंगदैर्ध्य λ=0.2 मी है
ऋणात्मक x दिशा में जिसका आयाम 0.25 मी और तरंगदैर्ध्य λ=0.2 मी है।
The correct Answer is:C
y=0.25sin(10πx−2πt) ...(i)
चूँकि समी (i) में (10πx) व (2πt) के बीच का चिह्न ऋणात्मक है, अतः तरंग धनात्मक x-दिशा में गतिमान है। समी (i) की व्यापक तरंग समीकरण से तुलना करने पर,
y=asin(kx−ωt)
यहाँ, a= आयाम, k = तरंग संख्या, ω=कोणीय आवृत्ति
समी (i) व (ii) से,
⇒2πT=2π⇒f=1 हर्ट्ज
तथा तरंगदैर्ध्य, λ=2π10π=0.2 मी
अतः तरंग धनात्मक x दिशा में आवृत्ति 1 हर्ट्ज और तरंगदैर्ध्य 0.2 मी के साथ गतिमान है।
अत: विकल्प (c) सही है।
Topper's Solved these Questions
Similar Questions
भँवर (Eddy) धाराएं बनती हैं जब
03:11View Solutionएक छात्र ने लोहे की छोटी सी गेंद के व्यास की माप 0.001 सेमी अल्पतांक वो स्क्रूगेज द्वारा की। यदि पैमाने की माप 5 मिमी और वृत्तीय पैमाने का शून्य संदर्भ लेवल से 25 भाग ऊपर है व स्क्रूगेज में शून्यांक त्रुटि 0.004 सेमी है तो गेंद का सही व्यास होगा
05:38View Solutionसमीकरण y=0.25sin(10πx−2πt) द्वारा प्रदर्शित तरंग, जहां X व् y मीटर में है तथा t सेकण्ड में है, चल रही है
02:49View SolutionA और B दो बिंदु है। बिंदुओं A और B के स्थिति क्रमशः 6¯a−2¯b और ¯b−9¯a है। वह अनुपात ज्ञात कीजिए जिसमें बिंदु P जिसका स्थिति सदिश ¯a−¯b है रेखाखण्ड AB को विभाजित करता है।
03:12View Solutionएक वाहन द्वारा t (सेकण्ड में) समय में कटी गई दुरी (मीटर में) समीकरण s=3t3+2t2+t+1 द्वारा दी जाती है। t=2 और t=4 के बीच त्वरण में अन्तर होगा
02:39View Solutionउस गोले का समीकरण ज्ञात कीजिए जिसका केन्द्र (2, 3, 1) है तथा जो समतल x + y + z = 0 को स्पर्श करता है।
View Solutiony=0.25sin(10πx−2πt) समीकरण जिसमे x और y मीटरो में है और t सेकंड में है, उस तरंग को व्यक्त करता है जिसका गतिपथ है :
View Solutionयदि '+' का अर्थ है '+', 'x' का अर्थ है '+',’-’ का अर्थ है 'x’ और ‘+’ का अर्थ है ‘-’ तब निम्नलिखित में से कौन-सा समीकरण सही है?
View SolutionX और Y अणुओं के संबंध में निम्नलिखित कथनों में से कौन सा गलत है?
View SolutionX और Y तत्वों द्वारा निर्मित एक यौगिक एक घनीय संरचना में क्रिस्टलीकृत होता है। जिसमें परमाणु X घन के कोनों पर होते हैं और परमाणु Y दो गैर-आसन्न फलक केंद्रों पर होते हैं। यौगिक का सूत्र है
View Solutionयदि Mn2+ में अयुग्मित इलेक्ट्रॉनों की संख्या 'X' है और +2 की तुलना में अन्य धनात्मक ऑक्सीकरण अवस्था 'Y' है। यहाँ x + Y का योग क्या है|
View Solutionएक आदर्श गैस के दस मोलों को एक बंद पात्र में भरा जाता है । पात्र में बेलन और पिस्टन के प्रकार की व्यवस्था है और 0.821 atm पर गैस का दाब स्थिर रहता है। निम्नलिखित में से कौन सा आलेख logV और logT के परिवर्तन का सही निरूपण करता है? (V= आयतन(लीटर में) और T= ताप (केलिवन में)
View Solutionएक क्रिस्टलीय ठोस X, Y और Z से बना है। घनीय निविड संकुलित (ccp) जालक में X के परमाणु उपस्थित हैं, Y सभी अष्टफलकीय रिक्तियों को ग्रहण करता है और Z सभी चतुष्फलकीय रिक्तियों को ग्रहण करता है। यदि एक काय विकर्ण के अनुदिश सभी परमाणुओं को हटा दिया जाता है, तो ठोस का सूत्र होगा :
View Solution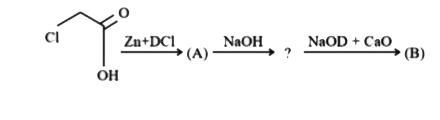
उपरोक्त दिए गए समीकरण में यौगिक (A) और (B) है :View Solutionअम्लीय माध्यम में H_2O_2, Cr_2O_(7)^(-2) को CrO_5 में परिवर्तित करता है, जिसमें दो (-O-O) बंध होते हैं। CrO_5 में Cr की ऑक्सीकरण अवस्था है :
View Solutionपरआयोडिक अम्ल, ग्लूकोस और फ्रक्टोस को फार्मेल्डिहाइड और फॉर्मिक अम्ल में विभाजित करता है। ग्लूकोस और फ्रक्टोस में फॉर्मिक अम्ल के मोलों का अनुपात होता है:
View Solution

