In case of inclusive classes the first step is to convert the same into exclusive classes by using adjustment value to change the limits ( See section 4.3.3.). Given the following frequency distribution with inclusive classes.

The adjustment value for converting inclusive classes into exclusive classes is 0.5(=6−52). Deduct 0.5 from all the lower limits and add 0.5 to all upper limits before applying the method of calculation.
Text Solution

l1=8.5
Δ1=8−5=3
Δ2=8−2=6
i=8.5−5.5=3
Substituting the values :
Mode =l1+Δ1Δ1+Δ2×i
=8.5+33+6×3=8.5+99=9.5
|
Topper's Solved these Questions
- MEDIAN AND MODEBook:SK AGGARWALAChapter:MEDIAN AND MODEExercise:Multiple Choice Questions
Explore 5 Videos
- MEDIAN AND MODEBook:SK AGGARWALAChapter:MEDIAN AND MODEExercise:Numerical Problem
Explore 21 Videos
- MEDIAN AND MODEBook:SK AGGARWALAChapter:MEDIAN AND MODEExercise:Numerical Problem
Explore 21 Videos
- MEASURES AND DISPERSIONBook:SK AGGARWALAChapter:MEASURES AND DISPERSIONExercise:Numerical Questions
Explore 18 Videos
- OTHER FORMS OF MARKETBook:SK AGGARWALAChapter:OTHER FORMS OF MARKETExercise:SAMPLE PAPER
Explore 29 Videos
Similar Questions
Knowledge Check
In the following frequency distribution, find the median class.

What is the upper limit of median class ?A150B160C155D165Consider the following frequency distribution

The upper limit of the median class inA17B17.5C18D18.5Consider the following frequency distribution of the height of 60 students of a class:
The upper limit of the median class in the given data is:
 A165B155C160D170
A165B155C160D170
In the following frequency distribution, what is the upper limit of the median class ?

View SolutionDetermine the upper limit of the modal class of the following frequency distribution:

View SolutionConsider the following frequency distribution:

the upper limit of the median class is
View SolutionFor the following raw data prepare a frequency distribution with a class interval of 5 on inclusive basis :
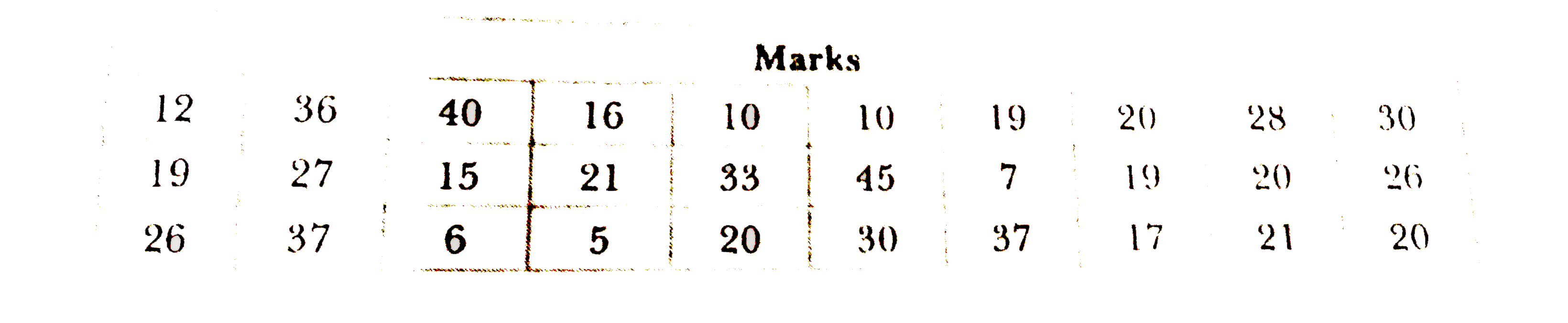
View SolutionConsider the following frequency distribution

The upper limit of the median class in
View Solution

