A solid sphere of radius R has a concentric cavity of radius R3 inside it. The sphere is found to just float in water with the highest point of it touching the water surface. Find the specific gravity of the material of the sphere.
VcavityVS=VS−VmetaVS=1−VmetaVS−(1)
(VS=Total volume of the sphere)
According to Archimedes. principle Weight of body = Weight of displaced liquid
mg=VSdwg⇒Vmetalg=VSdwg
(dS=Density of Solid matreial, dw=Density of Water)
VmetalVS=dwds−(2), From equation 1 and 2
∴VCavityVS=1−dwd=1−1ddw=1−1S.G
∴43π(R3)343πR3=1−1S.G⇒127=1−1S.G
⇒1S.G=1−127⇒S.G=2726
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EVALUATE YOURSELF - 1
2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EVALUATE YOURSELF - 2
2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Level 2 (H.W)
39 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
A solid sphere of radius 5 cm floats in water. If a maximum load of 0. kg can be put on it withot wetting the load find the specific gravityof the material of the sphere.
View Solutionblack colored solid sphere of radius "R" and mass "M" is inside a cavity with vacuum inside.The walls of the cavity are maintained at temperature T0 .The initial temperature of the sphere is 3T0 .If the specific heat of the material of the sphere varies as αT3 per unit mass with the temperature of the sphere,where α is a constant,then the time taken for the sphere to cool down to temperature 2T0 will be ( σ Stefan Boltzmann constant)
View Solution
Knowledge Check
A solid sphere of radius R has a concentric cavity of radius 'R/2' inside it. The sphere is found to just float in water with the highest point of it touching the water surface. The specific gravity of the material of the sphere is
A1B78C87D89Inside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
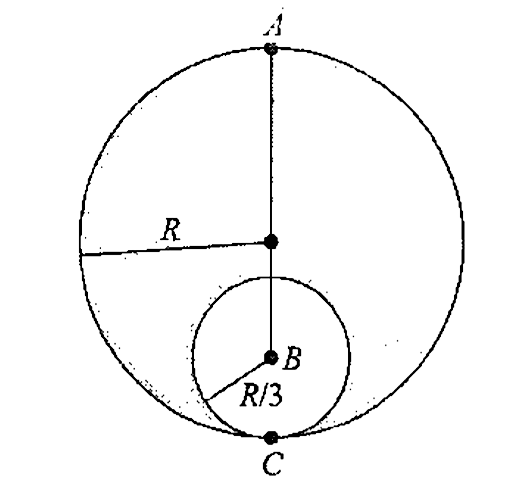 AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system onlyA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
 A(R2+R+1)(2–R)=1B(R2–R–1)(2–R)=1C(R2–R+1)(2–R)=1D(R2+R–1)(2–R)=1
A(R2+R+1)(2–R)=1B(R2–R–1)(2–R)=1C(R2–R+1)(2–R)=1D(R2+R–1)(2–R)=1
A solid sphere of radius 'R' has a cavity of radius R2. The solid part has a uniform charge density 'ρ' and cavity has no charge. Find the electric potential at point 'A'. Also find the electric field (only magnitude) at point 'C' inside the cavity
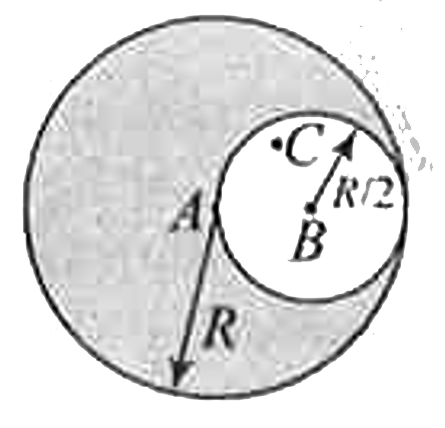
View SolutionA hollow sphere of external radius R and thickness t (< < R) is made of a metal of density ρ. The sphere will float in water if
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density σ is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be

View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?

View Solution
