A cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
a(a2ρg+k)
a(aρg+2k)
a(aρg2+2k)
a(a2ρg+k2)
The correct Answer is:D
Since, density of block =1/2 (density of water),
50% of its volume is immersed in water.
In the second case, half of the volume of the block is further immersed in water
W=Extra up thrust +spring force
=a×a×a2×2ρ×g+ka2=a(a2ρg+k2)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE - II (H.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND ITS APPLICATIONS)2videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE - II (H.W) (TORRICELLI.S THEOREM)6videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE - II (C.W) (EXCESS PRESSURE INSIDE A LIQUID DROP AND IN A SOAP BUBBLE)5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q13videos
MATHEMATICAL REVIEW & PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
Similar Questions
A cubical block 'A' of mass m0(=a3ρ=3kg) of edge 'a' and density ρ floats in a liquid of density 3ρ. The lower surface of the cube just touches the free end of massless spring of spring of spring constant k(=a2ρg) fixed at the bottom of the vessel. Another block 'B' of mass 'm' is lept over block 'A', so that is completely immersed in liquid without wetting the block 'B'. Then find the value of m in kg.
View SolutionA cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,View Solution
,View Solution
Knowledge Check
- Question 1 - Select One
A cubic block of side a is connected with two similar vertical springs as shown. Initially, bottom surface of the block of density σ touches the surface of the fluid of density 2σ while floating. A weight is placed on the block so that it is immersed half in the fluid, find the weight.
 Aa(K2=a2σg)Ba(K+a2σg)Ca(K+a22σg)Da2(K+a2σg)
Aa(K2=a2σg)Ba(K+a2σg)Ca(K+a22σg)Da2(K+a2σg) - Question 2 - Select One
A wooden block of mass 8 kg is tied to a string attached to the bottome of the tank. In the equilibrium the block is completely immersed in water. If relative density of wood is 0.8 and g=10ms−2, the tension T, in the string is
A120 NB100 NC80 ND20 N - Question 3 - Select One
Passage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
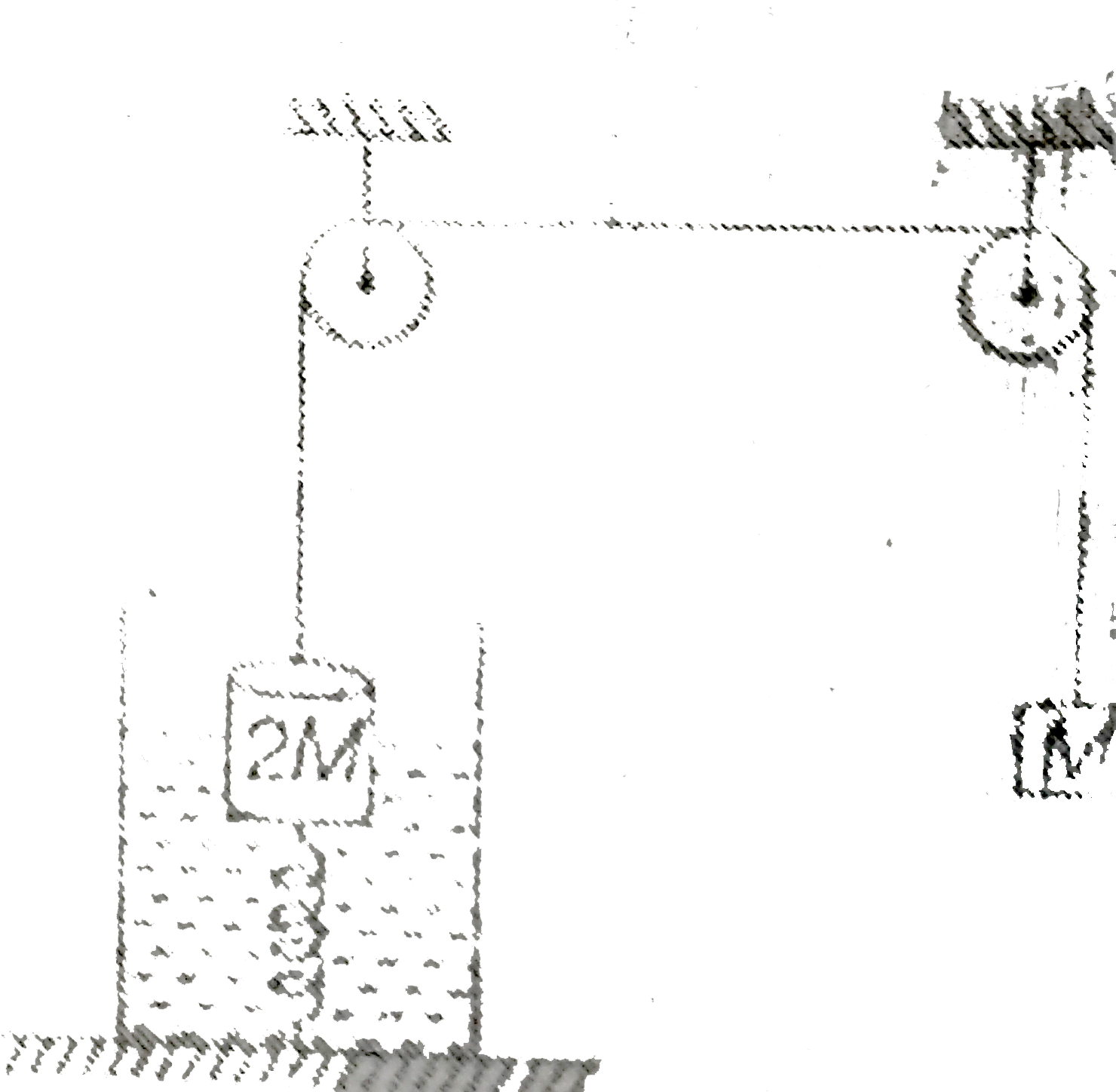
Under equilibrium conditionsAextensions of the spring is Mg3KBcompression of the spring is 2Mg3KCcompression of the spring is Mg8k)Dextension of the spring is Mg6k
A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,View Solution
,View SolutionA uniform cylindrical block of length l density d1 and area of cross section A floats in a liquid of density d2 contained in a vessel (d2>d1). The bottom of the cylinder just rests on a spring of contant k. The other end of the spring is fixed to the bottom of the vessel. A weight that may be placed on top of the cylinder such that the cylinder is just submerged in the liquid. find the weight.
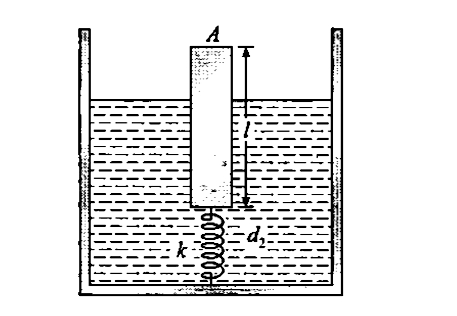 View Solution
View SolutionA wooden block of mass 0.5 kg and density 800 kgm−3 is fastened to the free end of a vetical spring of spring cosntant 50 Nm−1 fixed at the bottom. If the entire system is completely immersed in water, find a. the elongation (or compresion) of the spring in equilibrium and b. the time period of vertical oscillations of het block when it is slightly depressed and released.
View SolutionA cubical block of side 10cm floats at the interface of an oil and water as shown in the figure. The density of oil is 0.6gcm−3 and the lower face of ice cube is 2cm below the interface. The pressure above that of the atomosphere at the lower face of the block is
 View Solution
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)

By what maximum distance cylinder will be pushed downward into the liquid from equilibrium position so that when it is set free then tension in the string will not vanish [Assume at equilibrium position system was at rest]View Solution

