A travelling wave in the gas along the positive x-direction has an amplitude of 2cm, velocity 45m/s and frequency 75Hz. Particle acceleration after an interval of 3 sec at a distance of 135cm from the origin is
0.44×102cm/s2
4.4×105cm/s2
4.4×103cm/s2
44×105cm/s2
The correct Answer is:B
To find the particle acceleration after an interval of 3 seconds at a distance of 135 cm from the origin for a traveling wave in a gas, we can follow these steps:
1. Identify Given Values:
- Amplitude (A) = 2 cm = 0.02 m (convert to meters)
- Velocity (v) = 45 m/s
- Frequency (f) = 75 Hz
- Time (t) = 3 s
- Distance (x) = 135 cm = 1.35 m (convert to meters)
2. Calculate Angular Frequency (ω):
ω=2πf=2π×75=150π rad/s
3. Write the General Equation of the Wave:
The general equation for a traveling wave moving in the positive x-direction is:
y(x,t)=Asin(ωt−xv)
4. Substitute Values into the Wave Equation:
y(x,t)=0.02sin(150π×3−1.3545)
Calculate 1.3545=0.03:
y(x,t)=0.02sin(450π−0.03)
5. Calculate the Argument of the Sine Function:
450π−0.03 (This is approximately 450π since 0.03 is negligible compared to 450π)
The sine of any integer multiple of π is 0, but we need to consider the sine function's behavior around this value.
6. Calculate Velocity (v):
The velocity of the particle is given by:
v=∂y∂t=Aωcos(ωt−xv)
Substituting values:
v=0.02×150πcos(450π−0.03)
7. Calculate Acceleration (a):
The acceleration is given by:
a=∂v∂t=−Aω2sin(ωt−xv)
Substituting values:
a=−0.02×(150π)2sin(450π−0.03)
8. Evaluate the Sine Function:
Since 450π is an integer multiple of π, we can approximate:
sin(450π−0.03)≈sin(−0.03)≈−0.03 (using small angle approximation)
9. Calculate the Magnitude of Acceleration:
a=−0.02×(150π)2×(−0.03)
a=0.02×(150π)2×0.03
a=0.02×22500π2×0.03
a=0.02×675π2
10. Final Calculation:
a≈4.43×105 cm/s2
Final Answer:
The particle acceleration after an interval of 3 seconds at a distance of 135 cm from the origin is approximately 4.43×105 cm/s2.
- Amplitude (A) = 2 cm = 0.02 m (convert to meters)
- Velocity (v) = 45 m/s
- Frequency (f) = 75 Hz
- Time (t) = 3 s
- Distance (x) = 135 cm = 1.35 m (convert to meters)
ω=2πf=2π×75=150π rad/s
The general equation for a traveling wave moving in the positive x-direction is:
y(x,t)=Asin(ωt−xv)
y(x,t)=0.02sin(150π×3−1.3545)
Calculate 1.3545=0.03:
y(x,t)=0.02sin(450π−0.03)
450π−0.03 (This is approximately 450π since 0.03 is negligible compared to 450π)
The sine of any integer multiple of π is 0, but we need to consider the sine function's behavior around this value.
The velocity of the particle is given by:
v=∂y∂t=Aωcos(ωt−xv)
Substituting values:
v=0.02×150πcos(450π−0.03)
The acceleration is given by:
a=∂v∂t=−Aω2sin(ωt−xv)
Substituting values:
a=−0.02×(150π)2sin(450π−0.03)
Since 450π is an integer multiple of π, we can approximate:
sin(450π−0.03)≈sin(−0.03)≈−0.03 (using small angle approximation)
a=−0.02×(150π)2×(−0.03)
a=0.02×(150π)2×0.03
a=0.02×22500π2×0.03
a=0.02×675π2
a≈4.43×105 cm/s2
The particle acceleration after an interval of 3 seconds at a distance of 135 cm from the origin is approximately 4.43×105 cm/s2.
Topper's Solved these Questions
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Evaluate yourself-3
10 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Evaluate yourself-4
8 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Evaluate yourself-1
12 Videos
- VECTORSBOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-II (H.W)
14 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV
43 Videos
Similar Questions
A simple harmonic wave-train is travelling in a gas in the positive direction of the X-axis.Its amplitude is 2 cm, velocity 45ms−1 and frequency 75s−1.Write down the equation of the wave Find the displacement of the particle of the medium at a distance of 135 cm from the origin in the direction of the wave at the instant t=3 s.
View SolutionA sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
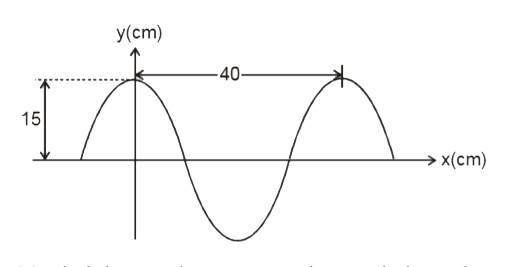
(b) Determine the phase constant ϕ, and write a general expression for the wave function.
View Solution
Knowledge Check
A particle performs harmonic oscillations along a straight line with a period of 6s and amplitude 4 cm. The mean velocity of the particle averaged over the time interval during which it travels a distance of 2 cm starting from the extreme position is
A1cms−1B2cms−1C4cms−1D8cms−1A progressive wave is travelling along the positive direction of the x-axis. For this wave, amplitude = 5 cm, period = 0.2 s and wavelength = 30 cm
The equation of the wave using SI units is given byAy=0.05sin2π(t0.2−x0.3)By=0.5sin2π(t0.2−x30)Cy=5sin2π(t0.2+x3)Dy=0.05sin2π(x0.3+t0.2)A wave travelling in the +ve x-direction having displacement along y-direction as 1m, wavelength 2π m and frequency of 1/π Hz is represented by
Ay=sin(2πx−2πt)By=sin(10πx−20πt)Cy=sin(2πx+2πtDy=sin(x−2t)
A sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
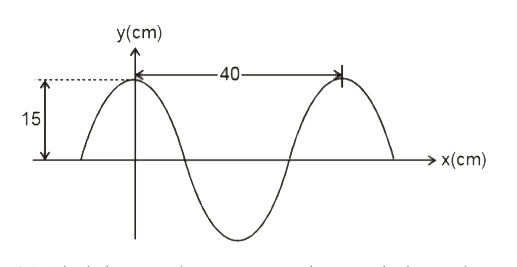
(a) Find the angular wave number, period angular frquency and speed of the wave.
View SolutionWrite the equation of a progressive wave propagating along the positive x-direction, whose amplitude is 5cm, frequency 250Hz and velocity 500 m/ s.
View SolutionA wave is propagating along the positive direction of X-axis. If the amplitude of wave is 10 cm, frequency 200 Hz and velocity 400 m/s, then write the equation of progressive wave.
View SolutionFor a progressive wave propagating along positive X-direction, amplitude, frequency and velocity are 10 cm, 300 Hz and 440 m/s, respectively. Write the equation of the wave.
View SolutionA travelling wave has the frequency v and the particle displacement amplitude A. For the wave the particle velocity amplitude is ………………… and the particle acceleration amplitude is ……………………..
View Solution
