A transverse wave is passing through a light string shown in fig.The equation of wave is y=Asin(wt−kx) the area of cross-section of string A and density is ρ the hanging mass is
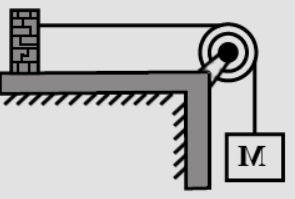
Aω
ωkg
ρAω2k2g
k2gω
The correct Answer is:C
V2=MgAρ, ω2K2=MgAρ
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-I (H.W)101videos
WAVES
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-II (C.W)15videos
WAVES
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - C.U.Q68videos
WAVES
- BOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-II (H.W)14videos
VECTORS
- BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV43videos
WORK , ENERGY & POWER
Similar Questions
Knowledge Check
- Question 1 - Select One or More
transverse simple harmonic wave is travelling on a string. The equation of the wave:
AIs the general equation for displacement of a particle of the string at any instant tBIs the equation ofthe shape ofthe string at any instant tCMust have sinusoidal formDIs an equation ofdisplacement for the particle at any one end at a particular time t - Question 2 - Select One
A wave travels on a light string. The equation of the wave is Y=Asin(kx−ωt+30∘+180∘). It is relected from a heavy string tied to an end of the light string at x=0. If 64% of the incident energy is reflected the equation of the reflected wave is
AY=0.8Asin(kx−ωt+30∘+180∘)BY=0.8Asin(kx+ωt+30∘+180∘)CY=0.8Asin(kx+ωt−30∘)DY=0.8Asin(kx+ωt+30∘) - Question 3 - Select One
A wave travels on a light string. The equation of the waves is y=Asin(kx−ωt+30∘). It is reflected from a heavy string tied to an end of the light string at x = 0. If 64% of the incident energy is reflected, then the equation of the reflected wave is
Ay=0.8Asin(kx−ωt+30∘+180∘)By=0.8Asin(kx+ωt+30∘+180∘)Cy=0.8Asin(kx−ωt−30∘)Dy=0.8Asin(kx−ωt+30∘)
A transverse wave propagating on the string can be described by the equation y=2sin(10x+300t) where x and y are in metres and t in second.If the vibrating string has linear density of 0.6×10−3gcm ,then the tension in the string is
View SolutionThe linear density of a vibrating string is 1.3×10−4kg/m A transverse wave is propagating on the string and is described by the equation y=0.021sin(x+30t) where x and y are measured in meter and tt in second the tension in the string is :-
View SolutionThe linear density of a vibrating string is 10−4kg/m. A transverse wave is propagating on the string, which is described by the equation y=0.02sin(x+30t), where x and y are in metres and time t in seconds. Then tension in the string is
View SolutionA travelling wave in a stretched string is described by the equation y=Asin(kx−ωt) the maximum particle velocity is
View SolutionThe linear density of a vibrating string is 2×10−4 kg/m. A transverse wave is propagating on the string and is described by the equation y=0.021 sin (x + 30 t) where x and y are in metre and t is in second. The tension in the string is
View Solution
