A wave of angular frequency 30 rad//sec propagates so that a certain phase of oscillationn moves along x-axis, y-axis , z-axis with speeds 1m/s, 2m/s and 2m/s respectively. The propagation constant K is
30ˆi+15ˆj+15ˆk
10ˆi+10ˆj+10ˆk
30ˆi+30ˆj+30ˆk
6ˆi+6ˆj+6ˆk
The correct Answer is:A
To find the propagation constant K for the given wave, we can follow these steps:
Step 1: Identify Given Values
- Angular frequency ω=30rad/s
- Velocity along the x-axis vx=1m/s
- Velocity along the y-axis vy=2m/s
- Velocity along the z-axis vz=2m/s
Step 2: Calculate Propagation Constant for Each Axis
The propagation constant K can be calculated using the formula:
K=ωv
For the x-axis:
Kx=ωvx=30rad/s1m/s=30rad/m
For the y-axis:
Ky=ωvy=30rad/s2m/s=15rad/m
For the z-axis:
Kz=ωvz=30rad/s2m/s=15rad/m
Step 3: Write the Propagation Constant Vector
The propagation constant vector K can be represented as:
K=Kx^i+Ky^j+Kz^k
Substituting the values calculated:
K=30^i+15^j+15^k
Final Answer
The propagation constant K for the wave is:
K=30^i+15^j+15^k(in rad/m)
---
- Angular frequency ω=30rad/s
- Velocity along the x-axis vx=1m/s
- Velocity along the y-axis vy=2m/s
- Velocity along the z-axis vz=2m/s
The propagation constant K can be calculated using the formula:
K=ωv
Kx=ωvx=30rad/s1m/s=30rad/m
Ky=ωvy=30rad/s2m/s=15rad/m
Kz=ωvz=30rad/s2m/s=15rad/m
The propagation constant vector K can be represented as:
K=Kx^i+Ky^j+Kz^k
K=30^i+15^j+15^k
The propagation constant K for the wave is:
K=30^i+15^j+15^k(in rad/m)
Topper's Solved these Questions
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-II (C.W)
15 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-II (H.W)
17 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-I (C.W)
104 Videos
- VECTORSBOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-II (H.W)
14 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV
43 Videos
Similar Questions
A plane wave of frquency ω propagates so that a certain phase of oscillation moves along the x,y,z axes with velocities υ1,υ2,υ3. Respectively. Find the wave vectork, assuming the unit vetors ex,ey,ez of the coordinate axes to be assigned.
View SolutionRepresent EM waves propagating along the x-axis in which electric and magnetic fields are along y-axis and z-axis respectively
View Solution
Knowledge Check
A wave of angular frequency ω propagates so that a certain phase of oscillation moves along x-axis, y-axis, z-axis with speeds c1c2 and c3 respectively.
Aω√c21+c22+c23(ˆi+ˆj+ˆk)Bωc1ˆi+ωc2ˆj+ωc3ˆkC(ωˆi+ωˆj+ωˆk)1cDNone of theseThree bodies having masses 5 kg, 4 kg and 2 kg is moving at the speed of 5 m/sand2m//s respectively along X-axis.The magnitude of velocity of centre of mass is
A1.0m/sB4m/sC0.9m/sD1.3m/sWhat are component of →g along x and y axis respectively |→g|=10m/s2.
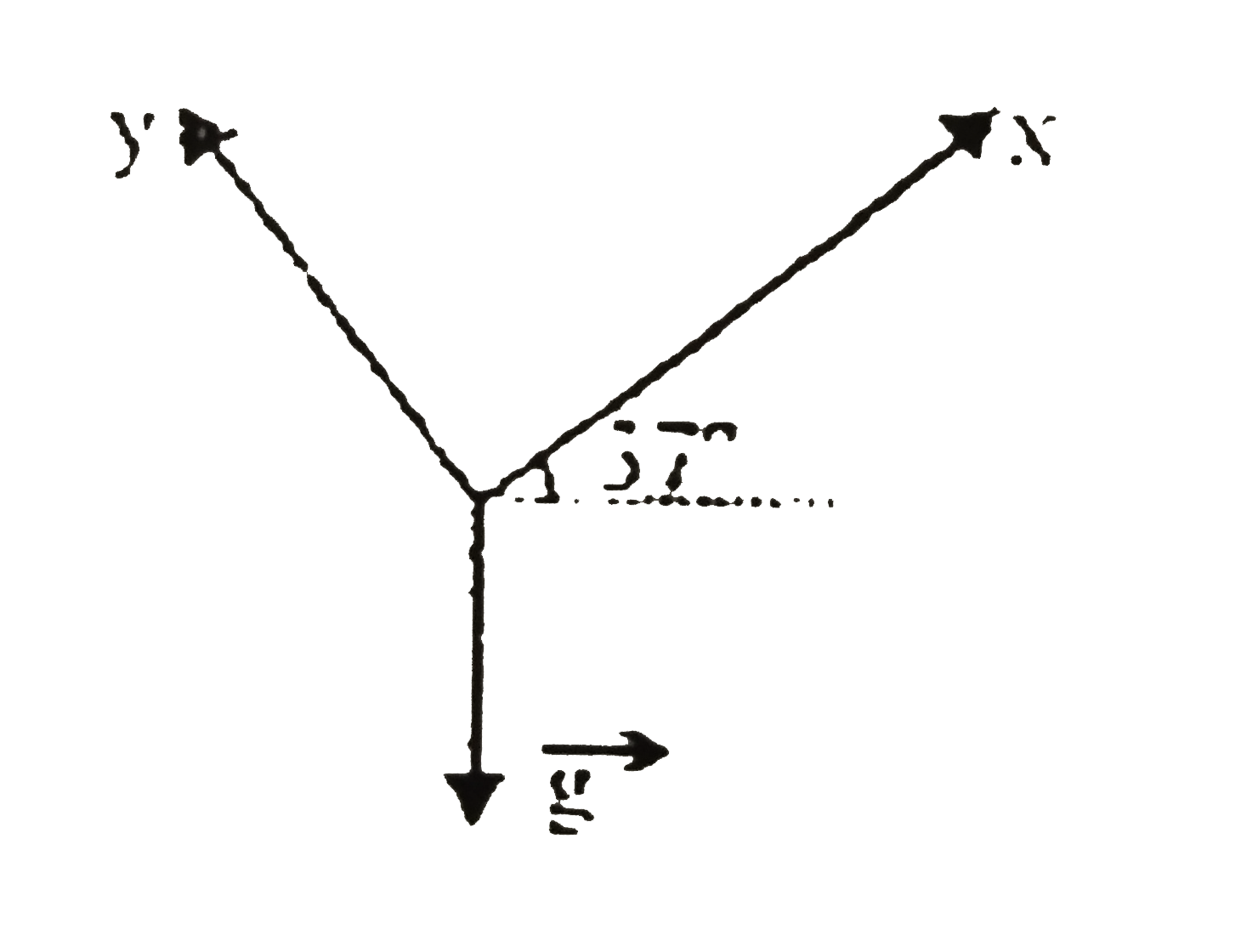 A(−6,−8)B(6,8)C(8,6)D(−3,−4)
A(−6,−8)B(6,8)C(8,6)D(−3,−4)
A plane harmonic wave of frequency 440 Hz propagates in a medium in a direction that makes angle 60∘C with x-axis as well as y-axis, find the phase difference between the oscillation at the point of medium whose coordinates are 91,1,2) and (2,3,1). the velocity of the wave in the medium is 220m/s.
View SolutionA gun is mounted on a trolley which can move uniformly with speed vm/s along the x-axis. Two shots are find from the origin with the gun making an angle 30∘ with the horizontal such that in the first case the trolley is moving along the positive x-axis and in the second case moving along the negative x- axis. The respective range of the projectile is 250m and 200m, along the x−axis. Find the velocity of the trolley in m/s. (Assume height of the trolley to be negligible)(given g=10m/s2).
View SolutionIf the particle in linear S.H.M. starts from the extreme left position, then its equation of motion is given by
View SolutionA particle is performing SHM along x-axis such that its acceleration along x-axis is : a=2−x where a is in m/s2 and x is in meter. If speed of the particle at x = 1 is zero in INCORRECT statement is :
View SolutionA shell at rest at the origin explodes into 3 fragments A,B and C of masses 1 kg, 2 kg and m kg respectively. A moves along the X-axis with a speed of 12 m/s, B moves along the Y-axis with a speed of 16 m/s and C flies off with a speed of 40 m/s. What is the total mass of the shell before explosion?
View Solution
