A steel wire of length 1m, mass 0.1kg and uniform cross-sectional area 10−6m2 is rigidly fixed at both ends. The temperature of the wire is lowered by 20∘C. If transverse waves are set up by plucking the string in the middle.Calculate the frequency of the fundamental mode of vibration.
Given for steel Y=2×1011N/m2
α=1.21×10−5per∘C
21Hz
42Hz
11Hz
22Hz
The correct Answer is:C
n=12L√T/μ=12L√YAαΔθμ
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-II (C.W)15videos
WAVES
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-II (H.W)17videos
WAVES
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-I (C.W)104videos
WAVES
- BOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-II (H.W)14videos
VECTORS
- BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV43videos
WORK , ENERGY & POWER
Similar Questions
Figure shows the shape of a string , the pairs of points which are in opposite phase is
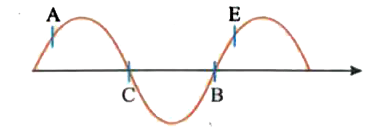 03:06View Solution
03:06View SolutionA transverse wave is travelling along a string from left to right. The figure below represents the shape of the string at a given instant. At this instant the points have an upward velocity are (here X-wave displacement, Y- particle displacement)
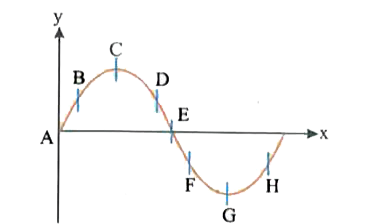 04:50View Solution
04:50View SolutionWhich of the following represents a progressive wave
04:53View SolutionA particle has a displacement of 12 m towards east then 5 m forwards north and then 6 m vertically upwards the resultant displacement is nearly
05:24View SolutionA large slab of mass 5kg lies on a smooth horizontal surface, with a block of mass 4kg lying on the top of it. The coefficient of friction between the block and the slab is 0.25. If the block is pulled horizontally by a force of F =6N, the work done by the force of friction on the slab, between the instants t=2s and t=3s, is (g=10ms−2)
 03:30View Solution
03:30View SolutionA steel wire of length 1m , mass 0.1kg and uniform cross-sectional area 10^(-6)m^(2) is rigidly fixed at both ends. The temperature of the wire is lowered by 20^(@)C . If transverse calculate the frequency of the fundamental mode of vibration. Given for steel Y = 2 xx 10^(11)N//m^(2) alpha = 1.21 xx 10^(-5) per ^(@)C
View SolutionA steel wire is rigidly fixed at both ends its length mass and cross sectional area are 1m, 0.1 kg and 106m2 respectively then the temperature of the wire is lowered by 20∘C if the transverse waves are setup by plucking the wire at 0.25m from one end and assuming that wire vibrates with minimum number of loops possible for such a case. Find the frequency of vibration (in Hz). [coefficient of linear expansion of steel =1.21×10−6/.∘C and young's modulus =2×1011/N/m2]
03:26View SolutionA load of 20kg is suspended by a steel wire in a sonometer experiment. Velocity of waves when the wire is rubbed with a resined cloth along the length is 20 times the velocity of waves in the same string, when it is plucked. Find area of cross-section of the wire, if Y for steel is 19.6xx10^(10)N//m^(2) and g =9.8m//s^(2) .
03:16View SolutionA steel wire of length 1 m and mass 0.1 kg and having a uniform cross-sectional area of 10^(-6) m^(2) is rigidly fixed at both ends. The temperature of the wire is lowered by 20^(@)C . If the wire is vibrating in fundamental mode, find the frequency (in Hz). (Y_(steel)=2xx 10^(11) N//m^(2),alpha_(steel)=1.21 xx 10^(-5)//.^(@)C) .
View SolutionA wire of length 1m is stretched by a force of 10N. The area of cross-section of the wire is 2 × 10^(–6) m^(2) and Y is 2 xx 10^(11) N//m^(2) . Increase in length of the wire will be -
03:25View SolutionA steel wire is rigidly fixed at both ends. Its length mass and cross-sectionl area are 1m, 0.1kg and 10−8m2 respectively. Tension in the wire is produced by lowering the temperature by 20∘C. If the transerverse waves are some up by plucking the wire at 0.25m from one end and assuming that the wire viberates with minimum number of loops possble for such a case. The frequency of viberation (in Hz) is found to be. 1.11. Find the value of K. Given α=1.21×10−5.∘C−1.Y−2×1011N/m2
 03:25View Solution
03:25View SolutionA steel wire of length 0.20m and uniform cross section 10^(-6)m^(2) is tied rigidly at both ends. The temperature of the wire is changed from 40^(@) C to 20^(@)C . Calculate the thermal tension in the wire given alpha =1.1. xx 10^(-5)//.^(@)C and Y=2xx10^(11)Nm^(-2)
03:46View SolutionA steel wire with a cross-sectional area 0.4mm2 is fixed tightly at 20∘C between two rigid supports. If the temperature falls to 0∘C, what will be the tension on the string? Given, for steel, Y =2×1012dyn⋅cm−2 and α=12×10−6∘C−1.
03:25View SolutionA steel wire of length 1 m, mass 0.1 kg and uniform cross sectional area 10^(-6)m^(2) is rigidly fixed at two ends. The temperature of the wire is lowered by 20^(@) C . If transverse waves are now set up by lucking the string at the middle, calculate the frequency of the fundamental tone. Givne, for steel, co-efficient of linear expansion = 1.21 xx 10^(-5_(@))C^(1) and Young's modulus = 2 xx 10 ^(11) N* m^(-2) .
02:32View SolutionA steel wire of length lm, mass 0.1 kg and uniform cross-sectional area 10−6m2 is rigidly fixed at both ends. The temperature of the wire is lowered by 200C. If the transverse waves are set up by plucking the string in the middle, calculate the frequency of the fundamental mode of vibration [Y=2×1011N/m2andα=1.21×10−5l0C]
06:26View SolutionA steel wire of length lm, mass 0.1 kg and uniform cross-sectional area 10^(-6)m^(2) is rigidly fixed at both ends. The temperature of the wire is lowered by 20^(0)C . If the transverse waves are set up by plucking the string in the middle, calculate the frequency of the fundamental mode of vibration [Y=2xx10^(11)N//m^(2) and alpha=1.21xx10^(-5)l^(0)C]
02:56View Solution

