In a sonometer wire, the tension is maintained by suspending a 20kg mass from the free end of the wire. The fundamental frequency of vibration is 300Hz.
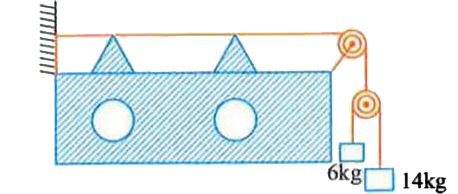
If the tension is provided by two masses of 6kg and 14kg suspended from a pulley as show in the figure the fundamental frequency will
still remain 300Hz
become larger
become smaller
decrease in the present situation and increase if the suspended masses of 6kg and 14kg are interchanged
The correct Answer is:C
Let a be the acceleration in the cord.
Then T−6g=6a
14g−T=14a
Adding both, 8g=20a⇒a=8g20
∴T=6×8g20+6g=6g(820+1)
The total effective tension in the sonometer wire T.=2T
When in the first case the tension was 20g. Hence, the effective tension is reduced.
Since f=12L√T.m
Topper's Solved these Questions
Similar Questions
In a sonometer wire, the tension is maintained by suspending a 50kg mass from the free end of the wire. The suspended mass is completely submerged in water, the fundamental frequency will become …………… Hz.
View SolutionA wire of length 2.00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
View Solution
Knowledge Check
In a sonometer wire, the tension is maintained by suspending a 50.7 kg mass from the free end of the wire. The suspended mass has a volume of 0.0075 m 3. The fundamental frequency of the wire is 260 Hz . If the suspended mass is completely submerged in water, the fundamental frequency will become (take g=10ms−2) [
A240 HzB230 HzC220 HzD200 HzThe tension in a sonometer wire is increased to nine times. Then the fundamental frequency of the wire is
A9 timesB3 timesC1/3 timesD1/9 timesFundamental frequency of sonometer wire is n. If the length, tension and diameter of wire are tripled the new fundamental frequency is
An√3Bn3Cn√3Dn3√3
A sonometer wire of length 1 m is stretched by a weight of 10 kg. The fundamental frequency of vibration is 100 Hz. Determine the linear density of material of wire.
View SolutionA wire under tension vibrates with a fundamental frequency of 600 Hz. If the length of the wire is doubled, the radius is halved and the wire is made to vibrate under one-ninth the tension. Then, the fundamental frequency will became
View SolutionTension applied to a wire of length 1m and its mass 1g, if it is to vibrate with the fundamental frequency of 50 Hz, will be
View SolutionFundamental frequency of sonometer wire is n. If the length, tension and diameter of wire are tripled. The new fundamental frequency is
View SolutionA sonometer wire of length 0.7 m is stretch by a weight of 4 kg. what is the linear density of the material of the wire, if its fundamental frequency is 200 Hz?
View Solution
