The time of flight of a projectile on an upwardd inctined plane depends upon
angle of inclination of the plane
angle of projection
the value of acceleration due to gravity
all of these.
The correct Answer is:D
To determine the time of flight of a projectile on an upward inclined plane, we can follow these steps:
1. Understand the Problem: We have a projectile launched at an angle α with respect to the horizontal, and it lands on an inclined plane that makes an angle θ with the horizontal.
2. Identify the Components of Motion:
- The initial velocity u can be broken down into two components:
- Horizontal component: ucosα
- Vertical component: usinα
3. Consider the Forces Acting on the Projectile:
- The gravitational force acting on the projectile is mg, which can be resolved into two components relative to the inclined plane:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
4. Determine the Acceleration:
- The acceleration of the projectile along the inclined plane due to gravity is gcosθ.
5. Use the Equation of Motion:
- The vertical displacement y can be expressed as:
y=usinα⋅t−12gcosθ⋅t2
- Since the projectile returns to the same vertical level when it hits the inclined plane, we set y=0:
0=usinα⋅t−12gcosθ⋅t2
6. Solve for Time of Flight:
- Rearranging the equation gives:
usinα⋅t=12gcosθ⋅t2
- Factoring out t (noting t≠0):
t(usinα−12gcosθ⋅t)=0
- This leads to:
t=2usinαgcosθ
7. Identify Dependencies:
- From the derived formula t=2usinαgcosθ, we can see that the time of flight t depends on:
- The angle of projection α
- The angle of inclination θ
- The acceleration due to gravity g
Conclusion:
The time of flight of a projectile on an upward inclined plane depends on the angle of projection α, the angle of inclination θ, and the gravitational acceleration g. Therefore, the correct answer is that it depends on all of these factors.
- The initial velocity u can be broken down into two components:
- Horizontal component: ucosα
- Vertical component: usinα
- The gravitational force acting on the projectile is mg, which can be resolved into two components relative to the inclined plane:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
- The acceleration of the projectile along the inclined plane due to gravity is gcosθ.
- The vertical displacement y can be expressed as:
y=usinα⋅t−12gcosθ⋅t2
- Since the projectile returns to the same vertical level when it hits the inclined plane, we set y=0:
0=usinα⋅t−12gcosθ⋅t2
- Rearranging the equation gives:
usinα⋅t=12gcosθ⋅t2
- Factoring out t (noting t≠0):
t(usinα−12gcosθ⋅t)=0
- This leads to:
t=2usinαgcosθ
- From the derived formula t=2usinαgcosθ, we can see that the time of flight t depends on:
- The angle of projection α
- The angle of inclination θ
- The acceleration due to gravity g
The time of flight of a projectile on an upward inclined plane depends on the angle of projection α, the angle of inclination θ, and the gravitational acceleration g. Therefore, the correct answer is that it depends on all of these factors.
Similar Questions
Knowledge Check
The time of flight of the projectile is:
Aa√2bgBa√bgC√2abgD√a2bg
In the figure shown, find.
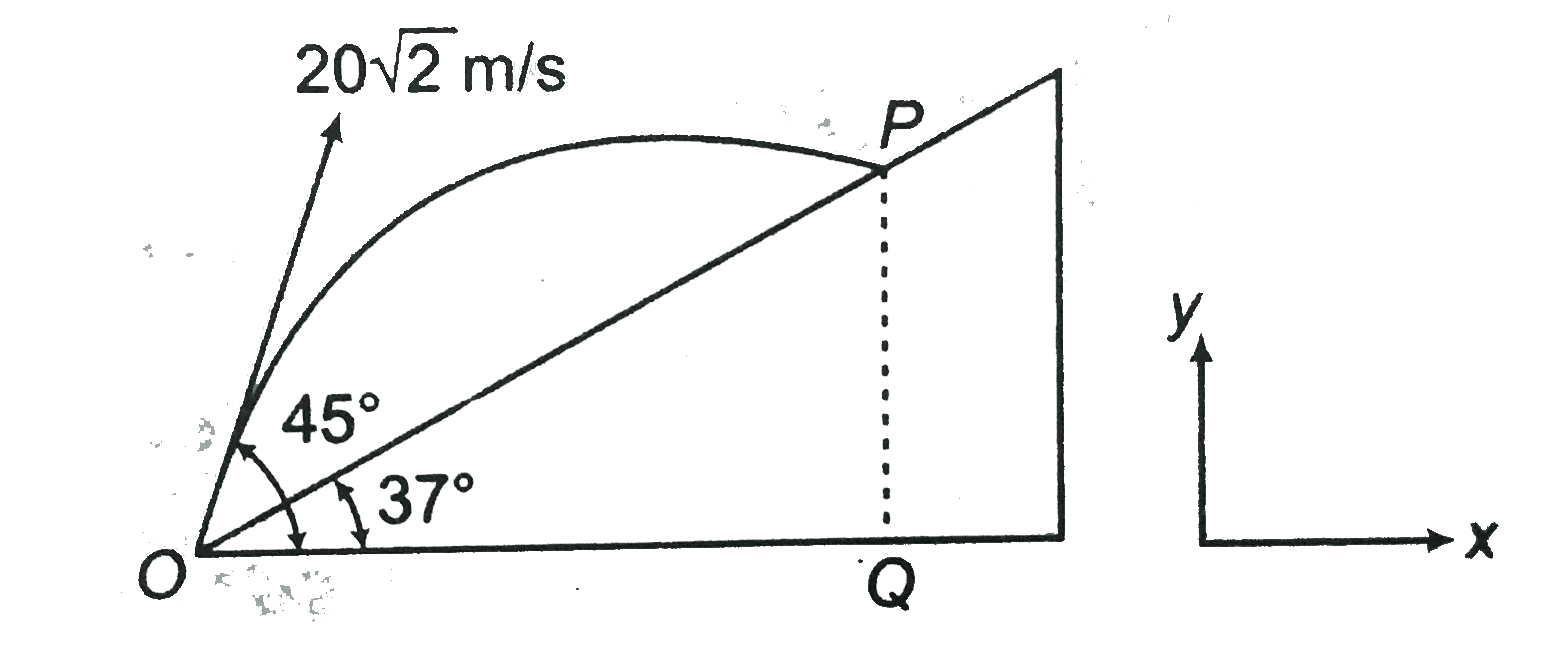
(a) time of flight of the projectile along the inclined plane.
(b) range OP.
View SolutionIn the figure shown, find.
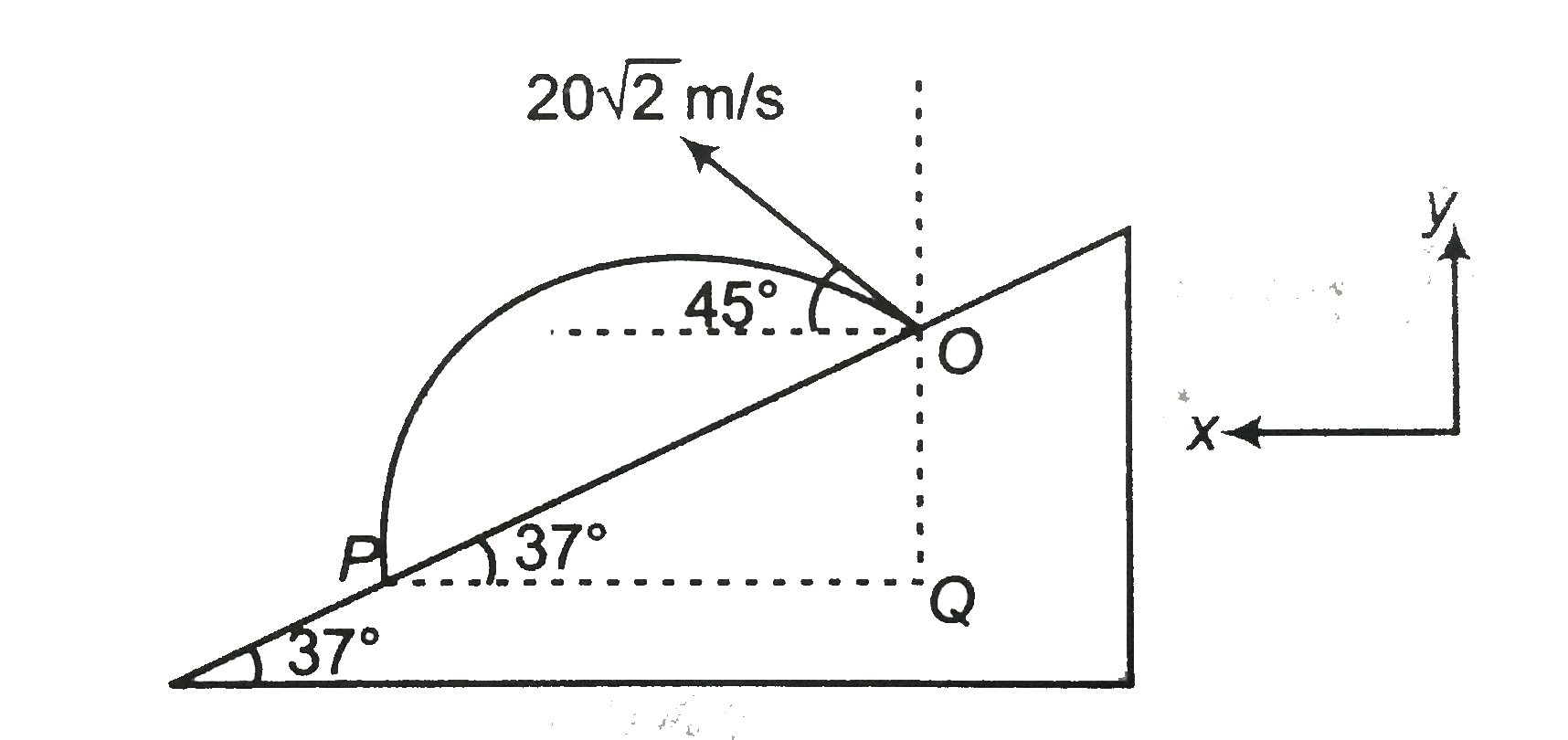
(a) time of flight of the projectile along the inclined plane.
(b) range OP.
View SolutionProjectile Motion - On An Inclined Plane
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)

View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
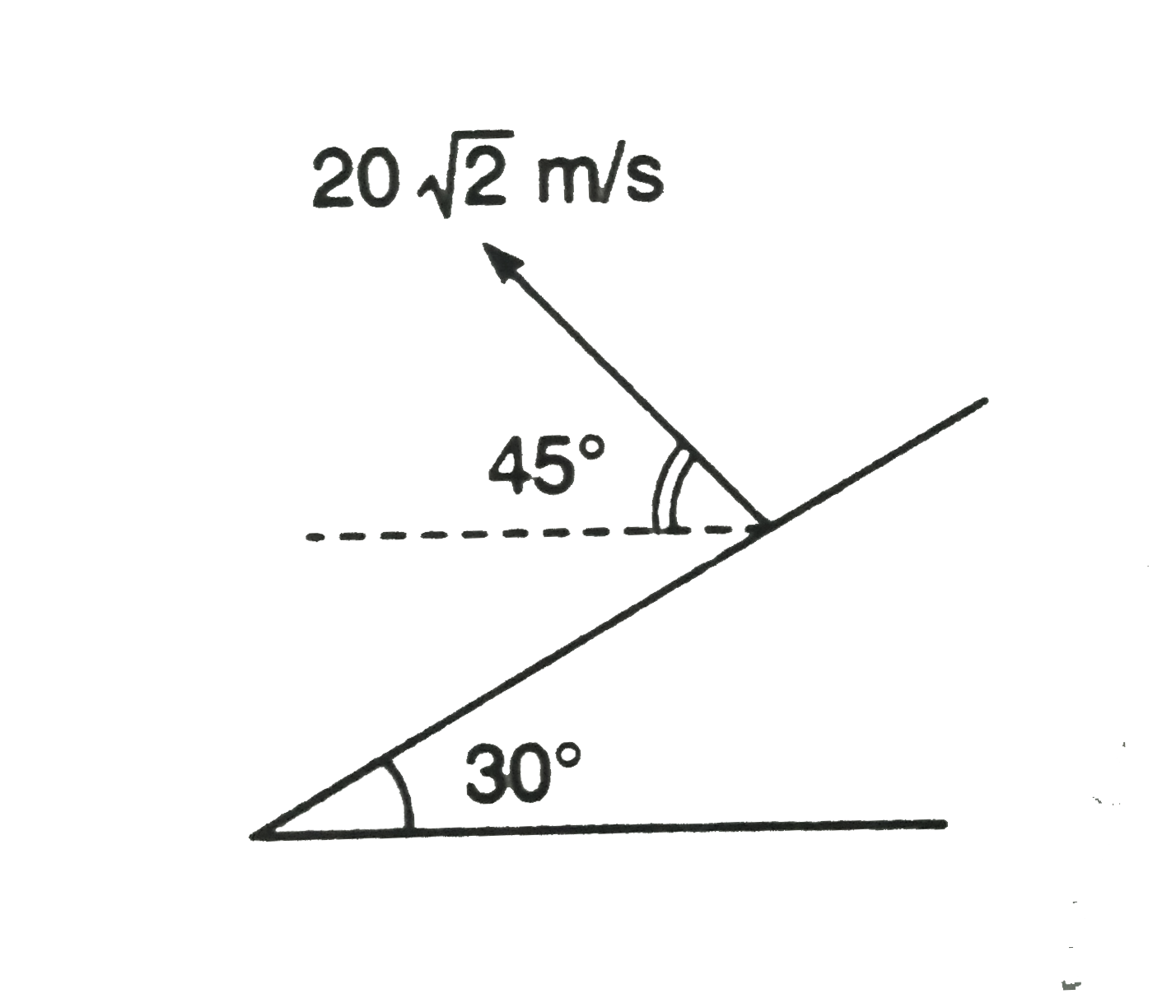
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
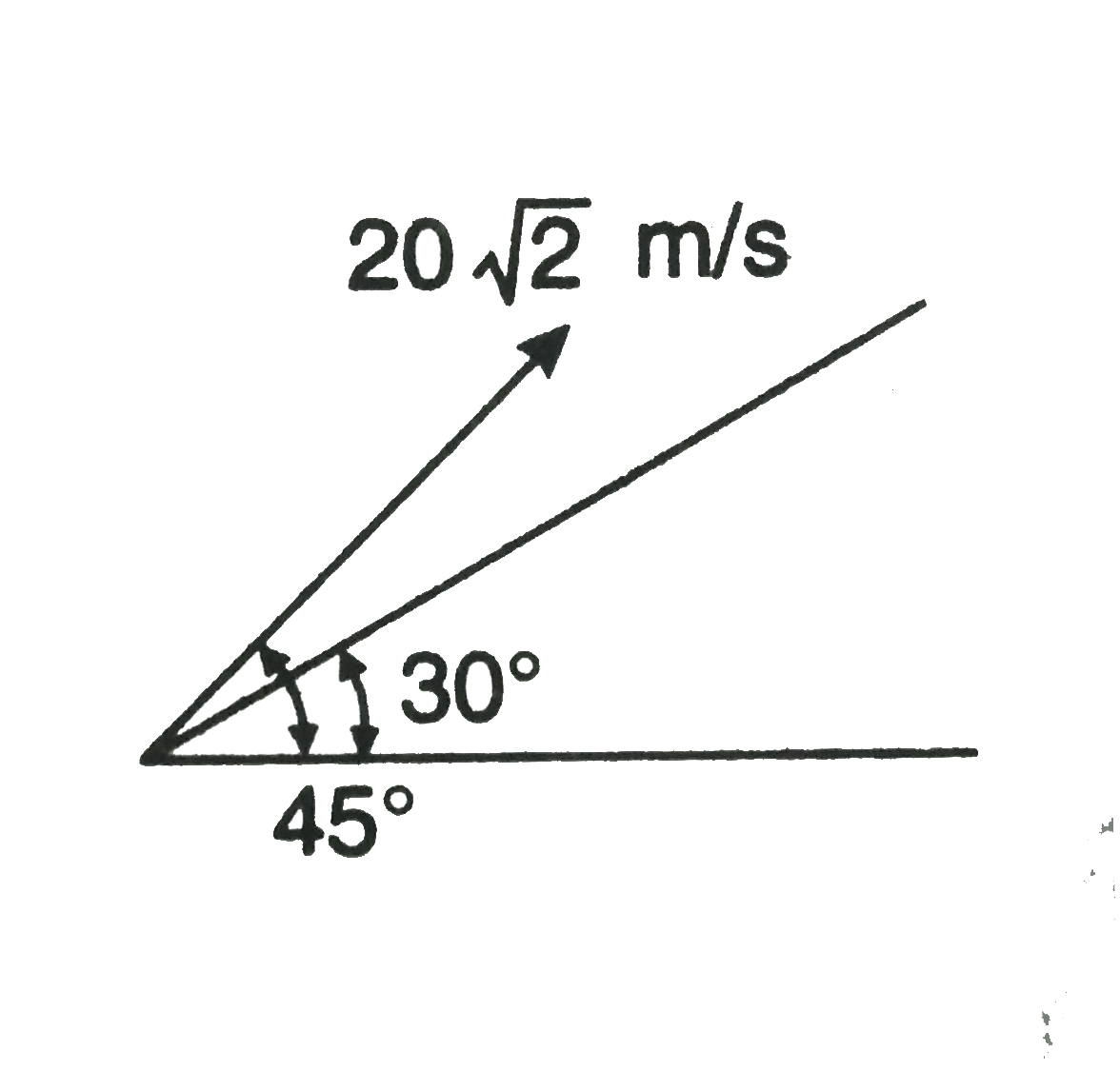
View SolutionThe time of flight of a projectile is related to its horizontal range by the equation gT2=2R.The angle of projection is?
View Solution

 .
.