A square loop of side 44 cm is changed to a circle in time 0.5 sec with its plane normal to a magnetic field 0.6 T. The emf induced is
0.5 V
0.4 V
0.2 V
0.6 V
The correct Answer is:D
To solve the problem, we need to calculate the induced electromotive force (emf) when a square loop is transformed into a circular loop while it is placed in a magnetic field. Here’s the step-by-step solution:
Step 1: Convert the side length of the square loop to meters
The side of the square loop is given as 44 cm. We need to convert this into meters.
Side length=44cm=44×10−2m=0.44m
Hint: Remember to convert all measurements to the same unit system, preferably SI units.
Step 2: Calculate the area of the square loop
The area As of the square loop can be calculated using the formula for the area of a square:
As=side2=(0.44)2=0.1936m2
Hint: The area of a square is calculated as the length of one side squared.
Step 3: Determine the circumference of the square loop
When the square loop is transformed into a circle, the perimeter of the square becomes the circumference of the circle. The perimeter P of the square is:
P=4×side=4×0.44=1.76m
Hint: The perimeter of a square is four times the length of one side.
Step 4: Calculate the radius of the circular loop
The circumference C of the circle is given by:
C=2πr
Setting the circumference equal to the perimeter of the square, we can solve for the radius r:
1.76=2πr⟹r=1.762π≈0.28m
Hint: To find the radius from the circumference, divide the circumference by 2π.
Step 5: Calculate the area of the circular loop
The area Ac of the circular loop can be calculated using the formula for the area of a circle:
Ac=πr2=π(0.28)2≈0.2464m2
Hint: The area of a circle is calculated as π times the radius squared.
Step 6: Calculate the change in magnetic flux
The magnetic flux Φ through the loop is given by:
Φ=B⋅A
Where B is the magnetic field strength (0.6 T) and A is the area of the loop. The change in magnetic flux ΔΦ when the loop changes from square to circle is:
ΔΦ=B⋅(Ac−As)=0.6⋅(0.2464−0.1936)≈0.6⋅0.0528=0.03168Wb
Hint: The change in flux is the difference between the final and initial areas multiplied by the magnetic field.
Step 7: Calculate the induced emf
The induced emf E can be calculated using Faraday's law of electromagnetic induction:
E=−ΔΦΔt
Given that the time Δt=0.5s:
E=−0.031680.5≈−0.06336V
Since emf is a magnitude, we take the absolute value:
E≈0.06336V
Hint: The negative sign indicates the direction of the induced emf according to Lenz's law, but we are interested in the magnitude.
Final Result
The induced emf when the square loop is changed to a circle is approximately 0.06336 V or 63.36 mV.
---
The side of the square loop is given as 44 cm. We need to convert this into meters.
The area As of the square loop can be calculated using the formula for the area of a square:
When the square loop is transformed into a circle, the perimeter of the square becomes the circumference of the circle. The perimeter P of the square is:
The circumference C of the circle is given by:
The area Ac of the circular loop can be calculated using the formula for the area of a circle:
The magnetic flux Φ through the loop is given by:
The induced emf E can be calculated using Faraday's law of electromagnetic induction:
The induced emf when the square loop is changed to a circle is approximately 0.06336 V or 63.36 mV.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-2 (C.W)
22 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-2 (H.W)
16 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-1 (C.W)
58 Videos
- ELECTRO MAGNETIC WAVESBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)
14 Videos
- ELECTROMAGNETIC WAVES BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -4
15 Videos
Similar Questions
A square loop of side 20 cm and resistance 0.30 Ω is placed in a magnetic field of 0.4 T. The magnetic field is at an angle of 45∘ to the plane of loop. If the magnetic field is reduced to zero in 0.5 s, then find the induced emf and induced current in the loop in this time interval.
View SolutionA circular loop of radius 10 cm is placed in a region of magnetic field of 0.5 T with its plane parallel to the magnetic field. Calculate the magnetic flux through the coil.
View Solution
Knowledge Check
A square loop of side 22cm is changed to a circle in time 0.4sec with its plane normal to a magnetic field 0.2T. The emf induced is
A+6.6mvB−6.6mvC+13.2mvD−13.2mvA square loop of side 10 cm and resistance 0.5 Ω is placed vertically in the East-West plane. A uniform magnetic field of 0.10 T is set-up across the plane in the North-East direction. The magnetic field is decreased to zero in 0.70 sat a steady rate. The magnitudes of induced emf and current during this time interval are
A0.1mV,2VB1mV,2mVC1V,2AD1mV,0.2AA square loop of side 22cm is converted into circular loop in 0.4s. A uniform magnetic field of 0.2Tdirected normal to the loop, then the induced in the loop is
A6.6×10−3VB6.6×10−5VC6.6×10−4VD6.6×10−8V
A square loop of side 10cm and resistance 0.5Ω is placed vertically in the east-west plane. A uniform magnetic field of 0.10T is set up across the plane in the north-east direction. The magnetic field is decreased to zero in 0.70s at a steady rate. The magnetude of current in this time-interval is.
View SolutionA square loop of side 10 cm and resistance 0.70 ohm is placed vertically in the east -west plane. A uniform magnetic field of 0.10 T is set up across the plane in north-east direction. The magnetic field is decreased to zero in 0.7 sec. at a steady rate. Determine the magnitudes of induced e.m.f. and current during this time interval.
View SolutionA square loop of side 10 cm and resistance 0.5 Ω is placed vertically in the east-west plane. A uniform magnetic field of 0.10 T is set up across the plane in the north-east direction. The magnetic field is decreased to zero in 0.70 s at a steady rate. Determine the magnitudes of induced emf and current during this time-interval.
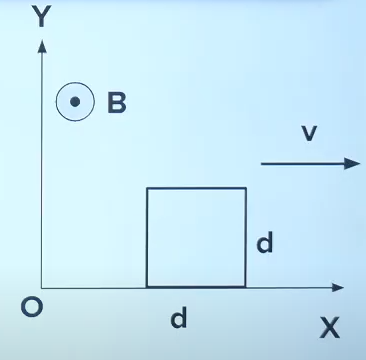
View SolutionA square loop of side d is moved with velocity vˆi in an non-uniform magnetic field B0axˆk then the emf induced shown is?
View SolutionA square coil of side 0.5m has movable sides. It si placed such that its plance is perpendiuclar to uniform magnetic field of induction 0.2T. If all the sides are allowed to move with a speed of 0.1m/s for 4 sec outwards, average induced emf is
View Solution
