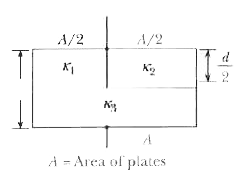
An air capacitor of capacitance C plate area A and plate separation d has been filled with three dielectrics of constant k1=3,k2=6 and k3=4 as shown in figure . What is the new capacitance ?

Shortcut method :
Before solving this problem try to understand the following concept . When a capacitor of capacitance C is divided into two parts in such a manner that each capacitor plate has area half of the earller vaue than each capacitor is understood to be connected in parallel and each one has value C/2 as shown below :
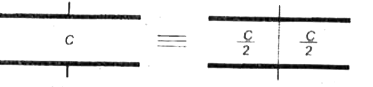
But if you divided the gap of the capacitor in two equal parts parallel to the plates then each one will have the capacitance 2 C (as d has been halved ) connected in series to each oither as shown below:

Now in the given question you can see the capacitor has been divided into three chambers viz. left half and the right half which is further into two part i.e upper half and lower half .

So all you have to do first is that write down the value of these separated chamgers in terms of C . Left half is C2 and right half C2 is multipled by 2 each for upper and lower half .

( That means right side C and C are in series and they are in parallel to C/2 making the entire capacitance C)
Now put the respective dielectrics in the chambers so each chamber will have its new value of capacitance K ( dielectric constant ) times the old value .
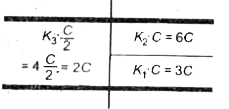
Now the right side 6 C and 3 C and in series so their equivalent value is 6C×3C6C×+3C =2C and this 2C is in parallel to the left side chamber capacitance 2 C . So the total capacitance becomes 4 C.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - TRY YOURSELF110videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT (SECTION-A) Objective Type Questions (Only one answer)47videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions25videos
ELECTROMAGNETIC WAVES
- BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)16videos
GRAVITATION
Similar Questions
A parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constant K1,K2 and K3 as shown in fig. If a single dielectric material is to be used to have the same effective capacitance as the above combination then its dielectric constant K is given by :
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be
 A4Aε0dB4.8Aε0dC5Aε0dD2.4Aε0d
A4Aε0dB4.8Aε0dC5Aε0dD2.4Aε0d - Question 2 - Select One
A parallel -plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials having dielectric constant k1,k2,k3 and k4 as shown in the figure below. If a single dielectric materical is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by
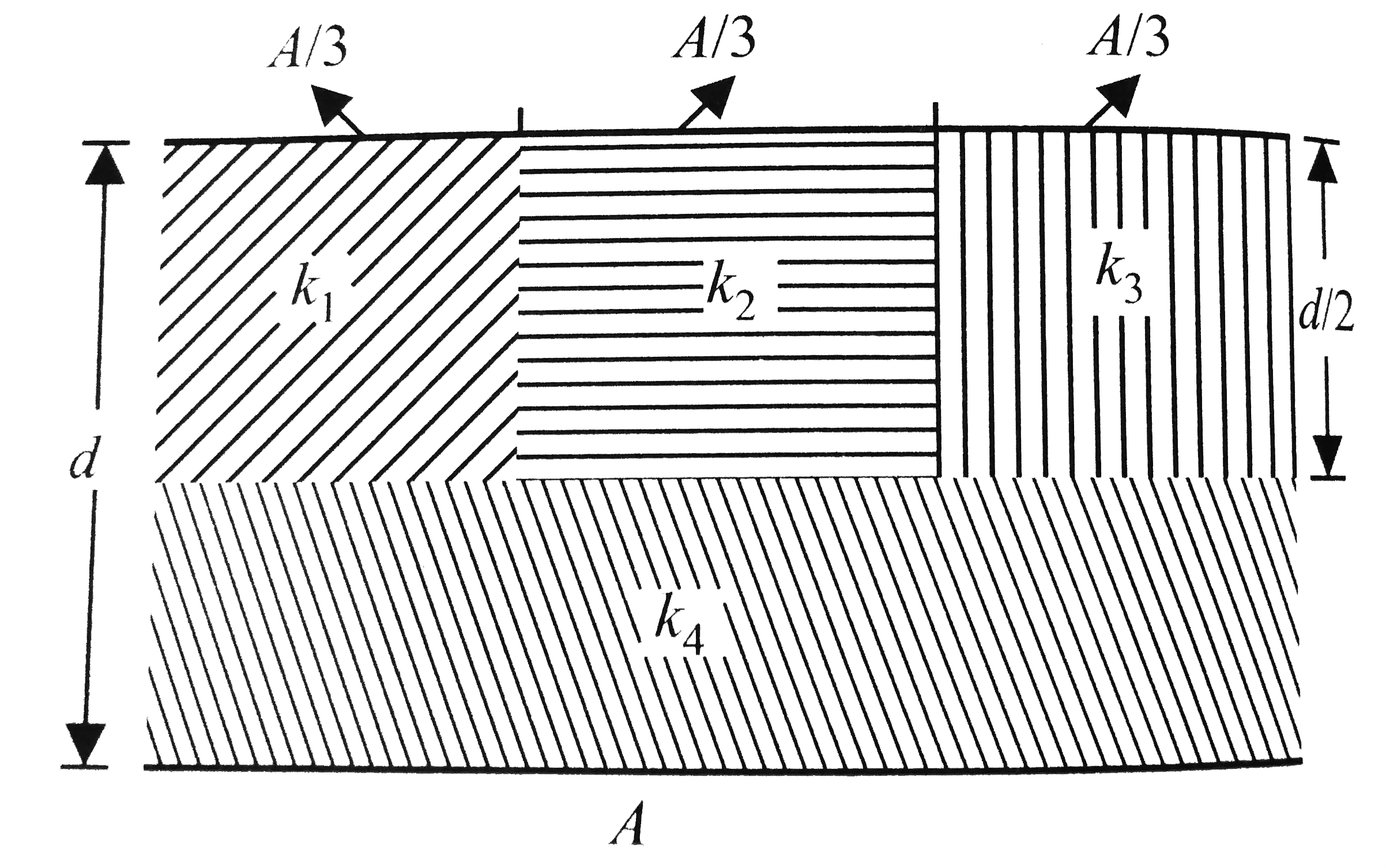 A2k=3k1+k2+k3+1k4B1k=1k1+1k2+1k3+32k4Ck=k1+k2+k3+3k4Dk=23(k1+k2+k3)+2k4
A2k=3k1+k2+k3+1k4B1k=1k1+1k2+1k3+32k4Ck=k1+k2+k3+3k4Dk=23(k1+k2+k3)+2k4 - Question 3 - Select One
A parallel -plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials having dielectric constant k1,k2,k3 and k4 as shown in the figure below. If a single dielectric materical is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by
 A2k=3k1+k2+k3+1k4B1k=1k1+1k2+1k1=32k4Ck=k1+k2+k+3k4Dk=23(k1+k2+k3)+2k4
A2k=3k1+k2+k3+1k4B1k=1k1+1k2+1k1=32k4Ck=k1+k2+k+3k4Dk=23(k1+k2+k3)+2k4
The capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
 View Solution
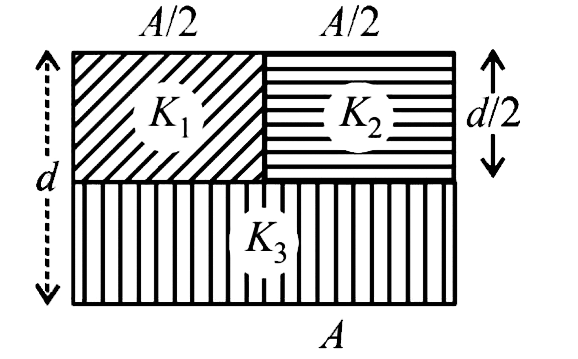
View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k1,k2 and k3 as shown. If a single dielectric naterial is to be used have the same capacitance C in this capacitor, then its dielectric constant k is given by
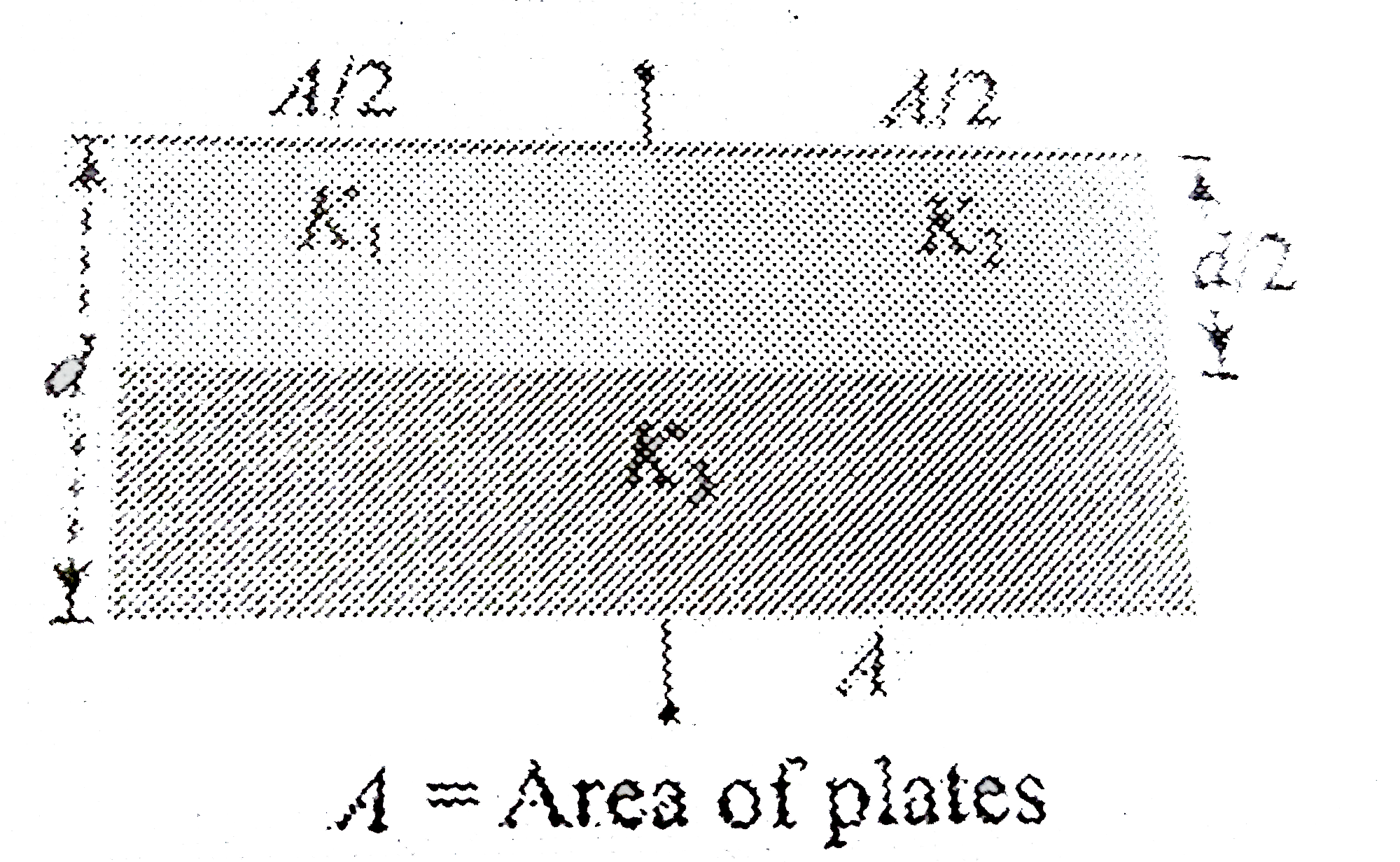 View Solution
View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k1k2andk3 as shown in the following figure. If a single dielectric material is to be used to have the same capacitance C in this capacitor then its dielectric constant k is given by
 View Solution
View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials hving dielectric constants K1,K2,K3 and K4 as shown in the figure below. If a single dielectric material is to be used to have the same capacitance c in this capacitor, then its dielectric constant K is given by
 View Solution
View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k1, k2 and k3 as shown. If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectic constant k is given by
 View Solution
View Solution

