Two concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
zero
(Q+q)rR
(Q−q)rR
qrR
To solve the problem of finding the final charge on the inner shell after connecting two concentric spherical conducting shells with charges q and Q, we can follow these steps:
Step 1: Understand the Initial Setup
We have two concentric spherical conducting shells:
- Inner shell with radius r and initial charge q.
- Outer shell with radius R and initial charge Q.
Step 2: Connect the Shells
When the two shells are connected by a conducting wire, charge can flow between them until they reach the same electric potential.
Step 3: Electric Potential of Conductors
For conductors, the electric potential V is constant throughout the conductor. The potential V at the surface of a spherical conductor is given by the formula:
V=k⋅Q′R
where k is Coulomb's constant, Q′ is the charge on the conductor, and R is its radius.
Step 4: Set Up the Equation for Potential
After connecting the shells, the potential on the inner shell (with charge q′) must equal the potential on the outer shell (with charge Q′):
Vinner=Vouter
This gives us:
k⋅q′r=k⋅Q′R
where q′ is the final charge on the inner shell and Q′ is the final charge on the outer shell.
Step 5: Conservation of Charge
The total charge before and after connecting the shells must be conserved. Therefore:
q+Q=q′+Q′
Step 6: Solve for Final Charges
From the potential equality, we can express Q′ in terms of q′:
Q′=Rrq′
Substituting Q′ into the conservation of charge equation:
q+Q=q′+Rrq′
q+Q=q′(1+Rr)
q′=q+Q1+Rr=q+Qr+Rr=r(q+Q)r+R
Step 7: Final Charge on Inner Shell
Thus, the final charge on the inner shell is:
q′=r(q+Q)r+R
Conclusion
The final charge on the inner shell after connecting the two conducting shells is:
r(q+Q)r+R
We have two concentric spherical conducting shells:
- Inner shell with radius r and initial charge q.
- Outer shell with radius R and initial charge Q.
When the two shells are connected by a conducting wire, charge can flow between them until they reach the same electric potential.
For conductors, the electric potential V is constant throughout the conductor. The potential V at the surface of a spherical conductor is given by the formula:
V=k⋅Q′R
where k is Coulomb's constant, Q′ is the charge on the conductor, and R is its radius.
After connecting the shells, the potential on the inner shell (with charge q′) must equal the potential on the outer shell (with charge Q′):
Vinner=Vouter
This gives us:
k⋅q′r=k⋅Q′R
where q′ is the final charge on the inner shell and Q′ is the final charge on the outer shell.
The total charge before and after connecting the shells must be conserved. Therefore:
q+Q=q′+Q′
From the potential equality, we can express Q′ in terms of q′:
Q′=Rrq′
q+Q=q′+Rrq′
q+Q=q′(1+Rr)
q′=q+Q1+Rr=q+Qr+Rr=r(q+Q)r+R
Thus, the final charge on the inner shell is:
q′=r(q+Q)r+R
The final charge on the inner shell after connecting the two conducting shells is:
r(q+Q)r+R
Similar Questions
Two concentric spherical conducting shells of radii R and 2R carry charges Q and 2Qrespectively.Change in electric potential on the outer shell when both are connected by a conducting wire is (k=(1)/(4 pi varepsilon_(0)))
View SolutionTwo concentric spherical conducting shells of radii R and 2R carry charges Q and 2Qrespectively.Change in electric potential on the outer shell when both are connected by a conducting wire is (k=14πɛ0)
View Solution
Knowledge Check
Two concentric conducting shells of radius a and b (b>a) carry charges Q and −2Q respectively. The correct variation of electric intensity E as a function of r is given by
A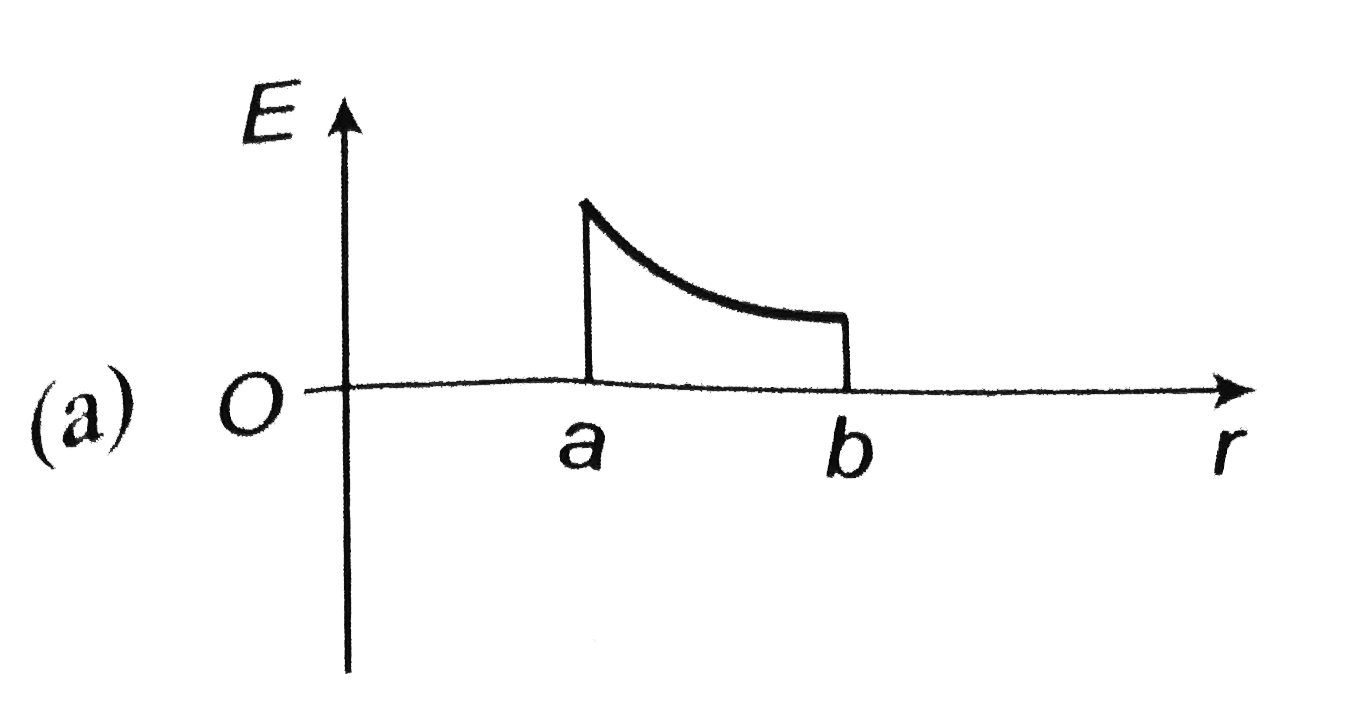 B
B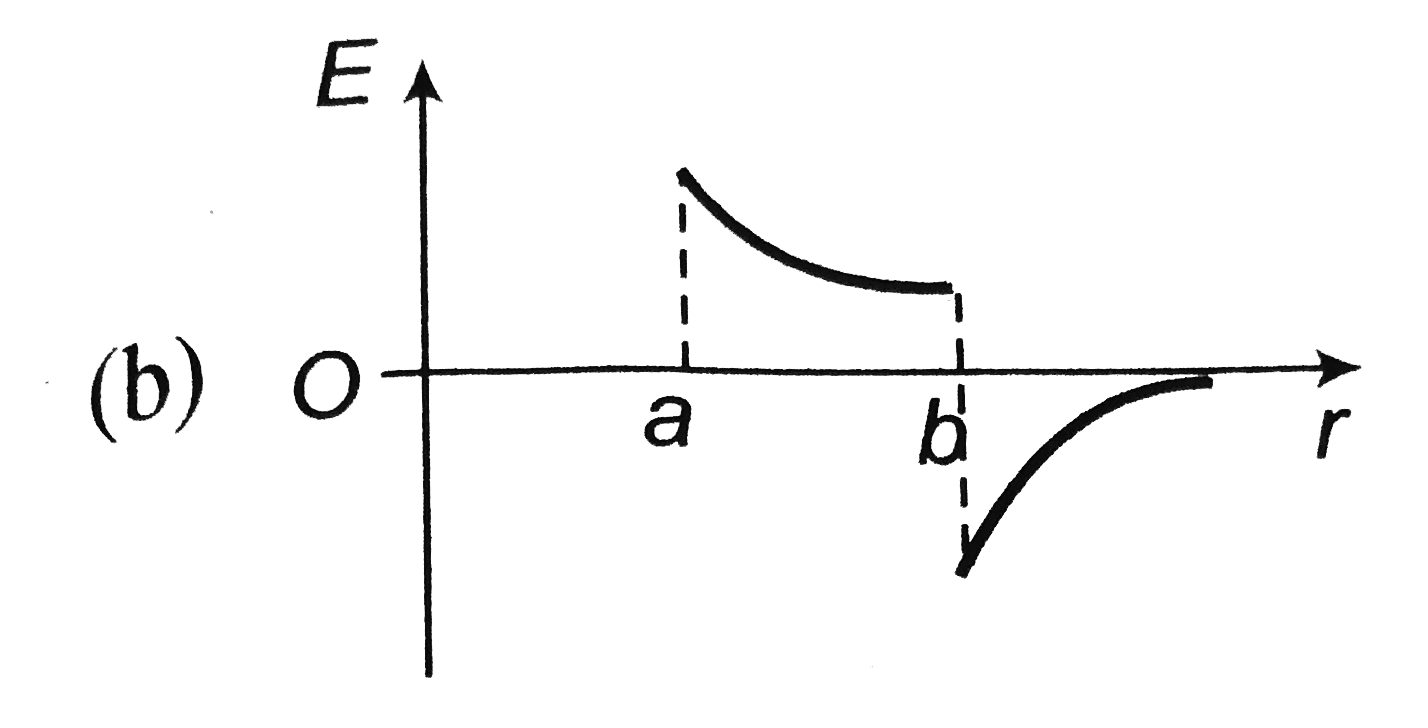 C
C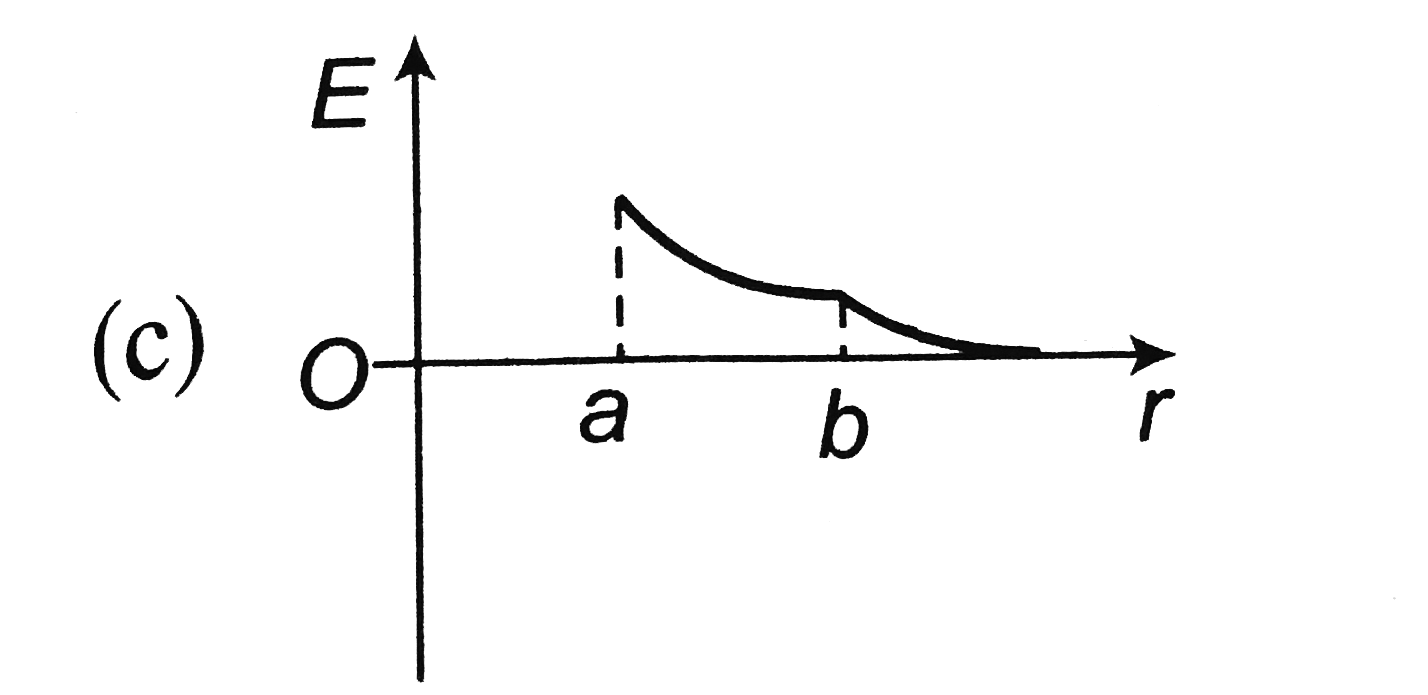 D
D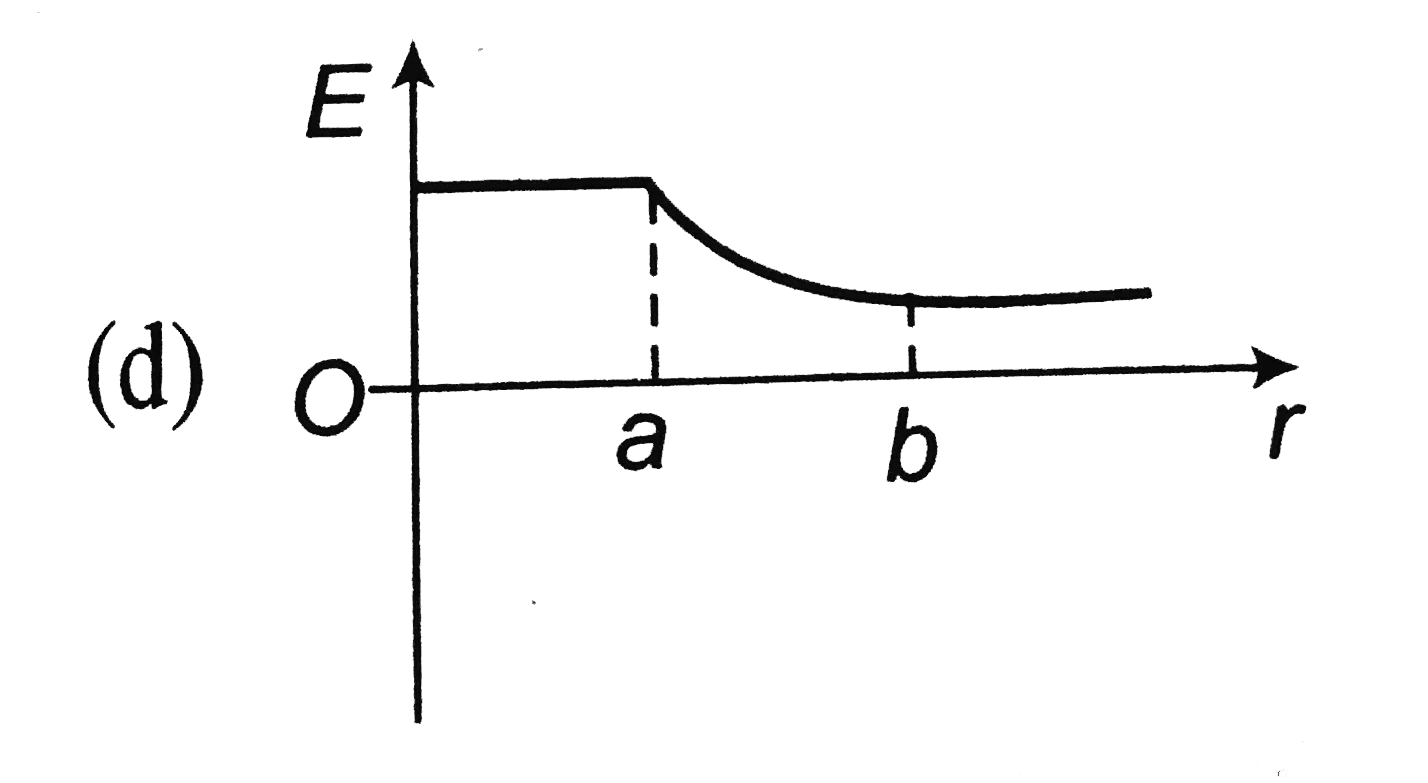
Three concentric conducting spherical shells have radii r, 2r, and 3r and charges q1,q2andq3, respectively. Innermost and outermost shells are earthed as shown in figure. The charges shown are after earthing. Select the correct alternative.
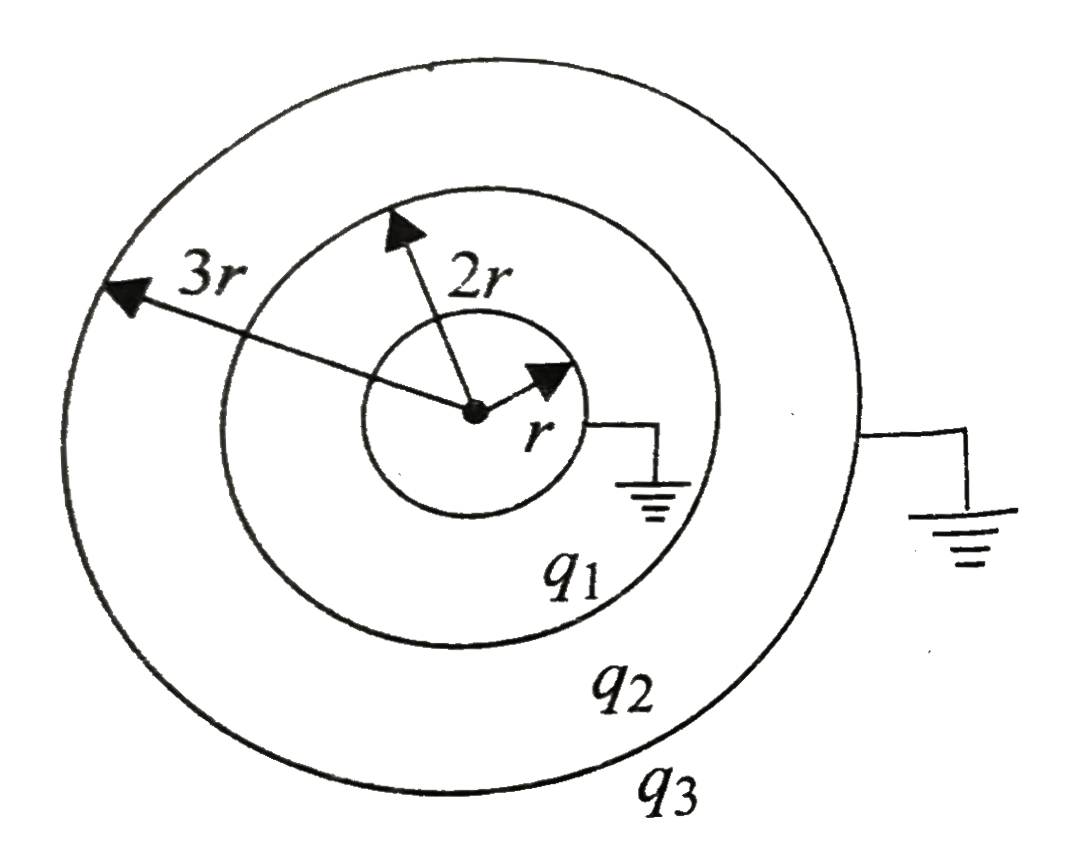 Aq1+q3=−q2Bq1=−q2Cq3q2=−13Dnone of these
Aq1+q3=−q2Bq1=−q2Cq3q2=−13Dnone of theseA spherical conducting shell of radius r0 carry a charge q0. Then value of electric field inside it is :-
Akq0/r2Bkq0/r3CzeroDuniform but non zero
Consider two concentric metalic shell's of radii R and 2R. The inner shell is having charge Q and outer shell is uncharged. If they are connected with a conducting wire. Then,
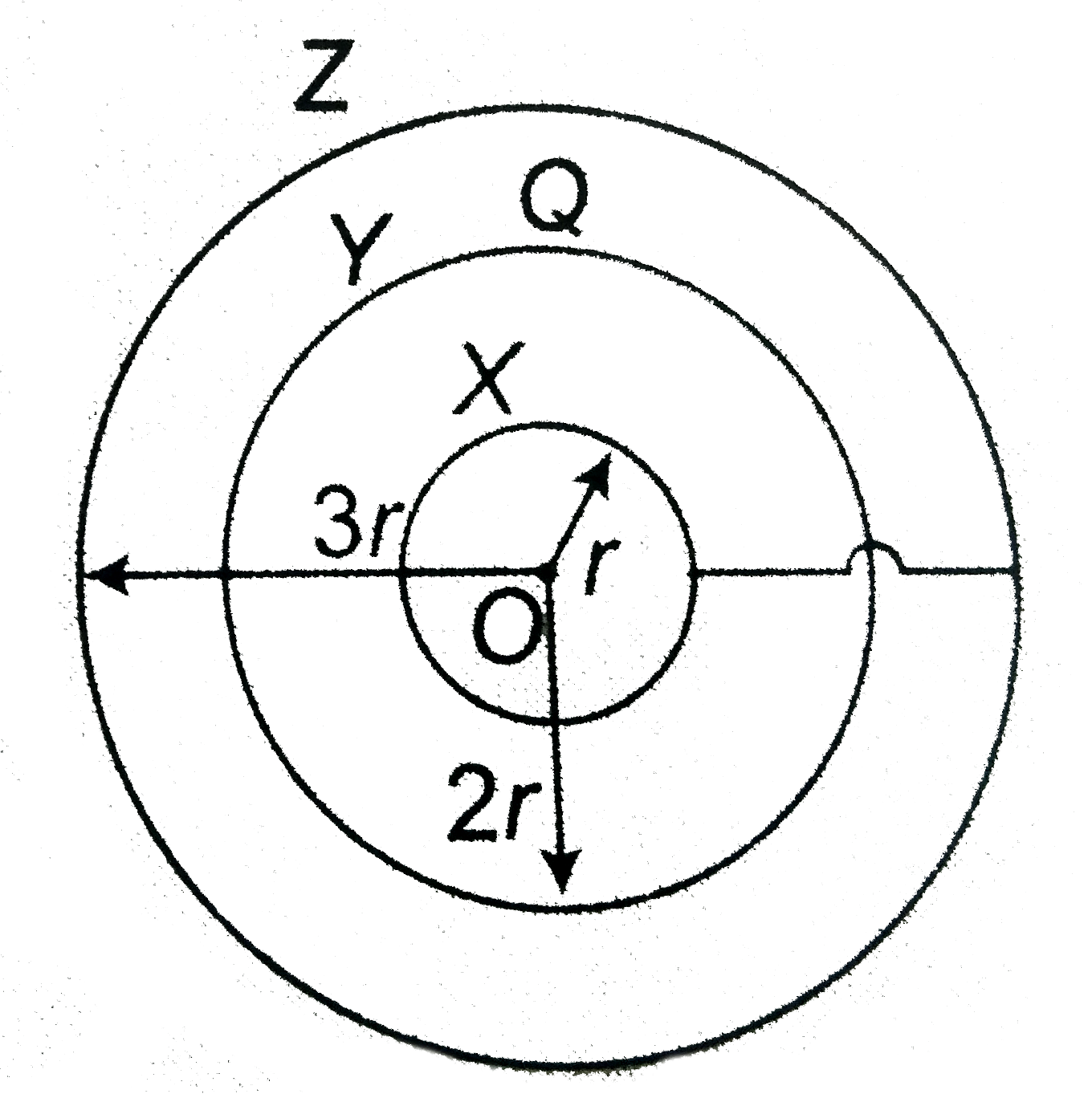
View SolutionThe figure shows three concentric , conducting ,spherical shells X,Y and Z with radii r,2r and 3r respectively . X and Z are connected by a conducting wire and Y is uniformly charged to charge Q. Find:
(a) charges on shells X and Z,
(b) potentials of Xand Y.
View SolutionTwo concentric conducting spheres of radii R and 3R carrying charges Q and 2Q respectively.If the charge on inner sphere is doubled.The potential difference between inner and outer spheres will..?
View SolutionA and B are two concentric spherical shells made of conductor. Their radii are R and 2R respectively. The two shells have charge Q and – 2Q on them. An electron escapes from the surface of the inner shell A and moves towards a small hole in the outer shell B. (a) What shall be the minimum kinetic energy of the emitted electron so that it can escape to infinity through the small hole in outer shell? (b) What will be your answer if charge on both the shells were +Q? Charge on electron = e.

View SolutionSurface charge densities of two thin concentric spherical capacitors or shells are given as σand−σ. The radii are R and 2R. The concentric capacitors are connected by a thin conducting wire. The entire charge on the inner miner transfers to the outer caspacitor and potential difference between them becomes zero. final potential of each capacitor will be
View Solution
